1. Chapitre 1 - Introduction▲
Le cours précédent d'Initiation Algorithmique a présenté les deux notions de problèmes et d'algorithme. Il a insisté sur différentes familles d'algorithmes (algorithme glouton, algorithme divide and conquer, programmation dynamique). Il a montré comment un même problème pouvait être résolu par des algorithmes différents appartenant à ces différentes familles. La qualité première attendue de ces algorithmes était leur correction.
Nous nous intéresserons ici plus particulièrement à une seconde qualité à savoir leur moindre coût en termes d'utilisation d'espace mémoire et de temps.
À cette fin, nous verrons comment représenter un ensemble dans une zone mémoire de la machine sur laquelle est exécuté un programme, et ce en définissant un objet intermédiaire : le type abstrait.
1-1. De l'abstrait au concret et inversement▲
Les problèmes algorithmiques rencontrés lors de ce semestre admettent pour entrée principalement un unique objet plus complexe que de simples éléments : l'objet ensemble.
Le modèle de calcul, c'est-à-dire la représentation conceptuelle de la machine sur laquelle sont exécutés les programmes, fournit une mémoire dont les accès en lecture et en écriture se font en temps constant pourvu que l'on ait l'adresse des octets à lire ou modifier. Ainsi, d'un point de vue théorique, la zone mémoire peut être considérée comme un immense tableau.
Les algorithmes que nous souhaitons écrire sont des algorithmes possédant la plupart des propriétés ci-dessous :
- leur indépendance vis-à-vis et de la machine et du langage de programmation dans lequel sera écrit le programme ;
- la simplicité d'écriture, qui permet leur compréhension et la preuve de leur correction ;
- leur faible complexité en temps et en espace.
En conséquence, les algorithmes ne seront pas écrits en code assembleur, mais dans un langage de haut niveau. Ainsi, dans un algorithme ne seront pas décrites les instructions de bas niveau accédant à telle ou telle adresse de la zone mémoire. Cette tâche est dévolue à des fonctions auxiliaires utilisées dans l'algorithme qui seront regroupées dans des ensembles logiques cohérents que nous nommons « types abstraits ».
Ainsi, entre l'objet mathématique très abstrait qu'est l'ensemble et l'objet très concret le tableau qui est la zone mémoire, nous concevrons et manipulerons :
- De nouveaux objets mathématiques plus structurés que l'ensemble, par exemple la séquence, la relation ;
- Des types abstraits qui réalisent cette interface entre un univers mathématique logique et un univers informatique calculatoire. Ainsi, chaque type abstrait sera un ensemble d'opérations défini logiquement et pouvant être implémenté à l'aide de programmes exécutables. Ces types abstraits auront pour nom l'ensemble, le tableau, la structure, la pile, la file, la liste, l'arbre binaire, le tas, etc.
1-2. Brefs rappels mathématiques▲
La connaissance et la maîtrise des notions suivantes sont indispensables. Se référer à tout ouvrage de mathématiques.
1-2-1. Ensemble▲
Un ensemble est un objet mathématique qui possède d'autres objets appelés ses éléments ; l'appartenance de l'élément kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp à l'ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp est noté kitxmlcodeinlinelatexdvpa \in Afinkitxmlcodeinlinelatexdvp.
L'ensemble vide, noté kitxmlcodeinlinelatexdvp\emptysetfinkitxmlcodeinlinelatexdvp, est l'unique ensemble ne contenant aucun élément.
Un singleton est un ensemble contenant un unique élément. Une paire est un ensemble contenant exactement deux éléments.
Notions et notations importantes
Intervalle, cardinalité, partie, opération union, intersection, différence, complément.
1-2-2. Relation binaire▲
Le produit cartésien de deux ensembles kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpBfinkitxmlcodeinlinelatexdvp est l'ensemble noté kitxmlcodeinlinelatexdvpA \times Bfinkitxmlcodeinlinelatexdvp ayant pour éléments tous les couples de la forme kitxmlcodeinlinelatexdvp(a, b)finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvpa \in Afinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpb \in Bfinkitxmlcodeinlinelatexdvp.
Une relation binaire kitxmlcodeinlinelatexdvprfinkitxmlcodeinlinelatexdvp définie sur kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpBfinkitxmlcodeinlinelatexdvp est une partie du produit cartésien kitxmlcodeinlinelatexdvpA \times Bfinkitxmlcodeinlinelatexdvp. L'appartenance kitxmlcodeinlinelatexdvp(a, b) \in rfinkitxmlcodeinlinelatexdvp est souvent notée kitxmlcodeinlinelatexdvpa\ r\ bfinkitxmlcodeinlinelatexdvp.
Notions et notations importantes
Réflexivité, associativité, symétrie, relation d'ordre (partiel ou total), relation bien fondé, relation d'équivalence, classes d'équivalence, les ensembles kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\mathbb{N}^*finkitxmlcodeinlinelatexdvp, intervalle d'entiers, relation d'arité kitxmlcodeinlinelatexdvpkfinkitxmlcodeinlinelatexdvp.
1-2-3. Fonction▲
Étant donnés deux ensembles kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpBfinkitxmlcodeinlinelatexdvp, une fonction kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp de kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp vers kitxmlcodeinlinelatexdvpBfinkitxmlcodeinlinelatexdvp est une relation binaire kitxmlcodeinlinelatexdvpr \subseteq A \times Bfinkitxmlcodeinlinelatexdvp telle que pour tout élément kitxmlcodeinlinelatexdvpa \in Afinkitxmlcodeinlinelatexdvp il existe un et un seul élément kitxmlcodeinlinelatexdvpb \in Bfinkitxmlcodeinlinelatexdvp tel que kitxmlcodeinlinelatexdvp(a, b) \in ffinkitxmlcodeinlinelatexdvp. L'appartenance kitxmlcodeinlinelatexdvp(a, b) \in ffinkitxmlcodeinlinelatexdvp est notée kitxmlcodeinlinelatexdvpf (a) = bfinkitxmlcodeinlinelatexdvp.
Notions et notations importantes
Injectivité, surjectivité, bijectivité, morphisme, isomorphisme, composition, restriction, inverse, involution, permutation.
1-2-4. Séquence▲
Une séquence à valeurs dans un ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp est une fonction de la forme kitxmlcodeinlinelatexdvps : \mathbb{N}^* \rightarrow Afinkitxmlcodeinlinelatexdvp ou de la forme kitxmlcodeinlinelatexdvps : [1,i] \rightarrow Afinkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvpi \in Nfinkitxmlcodeinlinelatexdvp. Dans ce dernier cas, la séquence kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp peut être notée kitxmlcodeinlinelatexdvp(s(1),\dots , s(i))finkitxmlcodeinlinelatexdvp, l'entier kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp éventuellement nul, est la longueur de kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp.
La séquence vide définie à partir de kitxmlcodeinlinelatexdvp[1,0] = \emptysetfinkitxmlcodeinlinelatexdvp est notée kitxmlcodeinlinelatexdvp()finkitxmlcodeinlinelatexdvp et est de longueur 0.
Notions et notations importantes
Sous-séquence extraite, concaténation, mot.
1-3. Un type abstrait : l'ensemble▲
Le type abstrait qui sera le fil conducteur de ce cours est le type ensemble. Sa signature est simplement :
|
estVide |
: ensemble |
→ booléen |
|
ensembleVide |
: |
→ ensemble |
|
appartient |
: élément x ensemble |
→ booléen |
|
ajouter |
: élément x ensemble |
→ ensemble |
|
enlever |
: élément x ensemble |
→ ensemble |
|
choisir |
: ensemble |
→ élément |
En supposant que l'on mette à votre disposition chacun des types cités, comment implémenter de façon optimale à l'aide de l'un de ces types ce type ensemble. Il n y a pas de réponse à une telle question. Tout dépend :
- D'informations supplémentaires sur la réalité des ensembles manipulés. Quelle est leur cardinalité ? Quelle est la cardinalité de leur univers ? Quelles sont les relations et opérations opérant sur les éléments de ces ensembles ?
- D'informations sur les opérations les manipulant ? Quelles sont les primitives jamais ou rarement utilisées ? souvent utilisées ?
- Et plus généralement de l'algorithme considéré.
Afin de faciliter l'écriture algorithmique, nous séparons :
- L'écriture d'un algorithme utilisant par exemple le type ensemble ;
- De l'implémentation du type ensemble et la compréhension de l'exécution machine de ses primitives.
Cette séparation est nécessaire dans une première étape et permet en distinguant les deux problèmes de pouvoir les résoudre plus facilement, car séparément. Dans la dernière étape conclusive, le choix de l'implémentation devra être justifié en considérant à la fois l'algorithme et l'implémentation et ainsi permettre d'évaluer le choix de cet algorithme et de cette implémentation en tentant de répondre à la question :
- est-ce que pour cet algorithme, cette implémentation permet d'avoir une complexité en temps (et ou en espace) optimale ?
- Est-ce que pour le problème considéré, cet algorithme et ce cette implémentation ont une une complexité en temps (et ou en espace) optimale ?
Deux familles d'implémentations
Cette section balaie très rapidement les liens entre différentes stratégies de représentation machine d'un ensemble et leurs liens avec les notions de séquence ou d'arbre.
L'implémentation d'un type abstrait sera réalisée à l'aide d'autres types abstraits. Cependant l'analyse des coûts en temps et en espace nécessite de comprendre la façon dont l'objet sera représenté in fine sur la machine. Rappelons que la mémoire est formée d'un nombre N de blocs de même taille, identifiés par des adresses ; l'accès au contenu de chacun de ces blocs à partir de son adresse se faisant en temps constant.
1-3-1. À taille constante▲
Une première classe d'implémentations machine sont celles qui utilisent un nombre de blocs constant pour mémoriser un ensemble de taille variable (pourvu qu'il ne dépasse pas une certaine cardinalité).
Tableaux de booléens
Une façon de représenter l'ensemble du dernier tirage au Loto {3, 7, 13, 19, 23, 25, 28} est d'utiliser le tableau de booléens à indices 1, […] , 49 suivant :
indices: 01 02 03 04 05 06 O07 08 09 10 11 12 13 14 15 16 17 18 19 20
valeurs: 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0
indices: 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
valeurs: 0 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
indices: 41 42 43 44 45 46 47 48 49
valeurs: 0 0 0 0 0 0 0 0 0L'avantage d'une telle représentation est de pouvoir exécuter les différentes primitives appartient, enlever, ajouter en temps constant. Constante qui dépend de l'accès à un bloc mémoire ; l'opération dure une fraction de seconde.
Les exécutions de estVide, ensVide, choisir sont ici aussi en temps constant ; mais une constante éventuellement importante, proportionnelle au nombre d'indices. En ajoutant un nouveau champ indiquant le nombre d'éléments de l'ensemble, nous obtenons une complexité en temps de estVide « petitement » constant.
Dans l'exemple ci-dessus, la solution est envisageable, car l'univers de tous les éléments possibles d'un ensemble est de cardinalité « proche » (49 dans l'exemple) de celle de l'ensemble (7 dans l'exemple).
Tables de hachage
Supposons que l'on s'intéresse à l'ensemble des patronymes français (que nous supposerons au nombre de 100 000 = 105 tirages).
Sachant qu'un caractère latin est codé à l'aide de 5 bits et qu'un patronyme possède au plus 20 caractères, on pourrait utiliser un tableau de booléens à ensemble d'indices 25…20 ≃ 1030. Le coût et la perte de mémoire sont alors prohibitifs (seul 10-23 % de l'espace est réellement utilisé !).
Une idée consiste à transformer selon une fonction de hachage kitxmlcodeinlinelatexdvph : \mathcal{A}^* \rightarrow [0, 10^6]finkitxmlcodeinlinelatexdvp chacun des noms en une valeur de taille inférieure par exemple ayant 6 digits (le nombre d'indices du tableau est ainsi ramené de 1030 à 106.
L'ensemble {PICCOLET D'HERMILLON, PICHAT,...} est ainsi représenté par le tableau
indices : ... h(PICCOLET D'HERMILLON) ... h(PICHAT)
valeurs : ... PICCOLET D'HERMILLON ... PICHATObservons qu'avec une telle représentation, toutes les « bonnes » propriétés du tableau à valeurs booléennes sont conservées. Les opérations sont à coût constant.
Une première difficulté apparaît : l'existence de collisions à savoir des tirages kitxmlcodeinlinelatexdvpt \ne ufinkitxmlcodeinlinelatexdvp ayant même hachés (kitxmlcodeinlinelatexdvph(t) = h(u)finkitxmlcodeinlinelatexdvp).
1-3-2. À taille proportionnelle à la cardinalité de l'ensemble représenté▲
Différents choix s'offrent alors.
1-3-3. Représentations par une « séquence »▲
Une façon naturelle de représenter tout ensemble par une séquence : c'est-à-dire par exemple, représenter l'ensemble {3, 7, 13, 19, 23, 25,28} par la séquence (13, 23, 3, 7, 28, 25, 19). Observons ici les différents choix qui s'offrent selon que :
- On autorise ou non la duplication des éléments. A-t-on intérêt à représenter {3, 7, 13, 19, 23, 25, 28} par la séquence (3, 7, 13, 19, 13, 19, 28, 3, 3, 23, 25, 28) ?
- On impose ou non que les éléments apparaissent dans la séquence en respectant l'éventuel ordre total de l'ensemble. A-t-on intérêt à représenter {3, 7, 13, 19, 23, 25, 28} par la séquence (3, 7, 13, 19, 23, 25, 28) ?
Les types abstraits permettant d'implémenter de telles séquences ne manquent pas :
- Le type Tableau ;
- Le type Pile ;
- Le type File ;
- Le type Liste.
Représentation contiguë
Une première technique pour représenter la liste (3, 7, 13, 19, 23, 25, 28) est d'utiliser 7 blocs mémoire contigus dont les adresses définissent intrinsèquement l'ordre des éléments qu'elles contiennent.
La liste (3, 7, 13, 19, 23, 25, 28) peut ainsi avoir pour représentation machine :
adresses 12123 12124 12125 12126 12127 12128 12129
contenus 3 7 13 19 23 25 28Cette représentation est la représentation naturelle du type Tableau ; cette proximité entre ce type et cette implémentation ne doit cependant pas être considérée comme absolue : en conclusion de ce chapitre, nous verrons pourquoi représenter des tableaux sous la forme de listes chaînées !
L'un des inconvénients d'une telle représentation est la gestion de cet espace mémoire. Si au cours de l'exécution de votre algorithme, vous souhaitiez augmenter l'ensemble {3, 7, 13, 19, 23, 25, 28} d'un seul élément et si les blocs se trouvant aux adresses 12122 et 12130 n'étaient pas libres, il serait alors nécessaire de trouver un minimum de 8 blocs contigus libres et de recopier tous les éléments.
Représentation par chaînage
Une technique pour implémenter l'un de ces types est le chaînage c'est-à-dire d'accoler à l'élément de la séquence l'adresse de l'élément qui lui succède. Ainsi la séquence (13, 23, 3, 7, 28, 25, 19) aura par exemple pour représentation-machine l'ensemble des blocs d'adresses respectives :
adresses 12123 12231 13213 34548 90808 98773 98799ayant respectivement pour contenu :
contenus 28:90808 7:12123 23:98799 13:13213 25:98773 19 :------ 3:12231L'avantage d'une telle méthode est de pouvoir en temps contant :
- Supprimer un élément de la séquence, pourvu que l'on ait son adresse ;
- Ajouter un élément qui n'est pas déjà présent dans la séquence ;
- Tester si une séquence est vide ;
- Créer une liste vide.
L'un des inconvénients est de se mettre en situation de parcourir jusqu'à la séquence tout entière pour :
- Pour décider si un élément s'y trouve ;
- Calculer l'adresse d'un élément de cette séquence.
1-3-4. Représentation par un arbre▲
Décider en temps linéaire l'appartenance d'un élément à un ensemble étant un handicap, une alternative convaincante à la structure unidimensionnelle qu'est la séquence, c'est l'arbre, un objet bidimensionnel.
Différentes sortes d'arbres existent. Ceux étudiés dans ce cours seront tous « enracinés », c'est-à-dire possédant un sommet singulier appelé la « racine » de l'arbre. Citons-en quelques-uns :
- les arbres binaires de recherche ;
- les arbres rouges et noirs, une variante des précédents ;
- les tas.
L'idée commune à ces arbres est d'utiliser les propriétés relatives des éléments (en supposant qu'ils sont munis d'un ordre total : ce qui peut toujours être supposé) pour les placer intelligemment dans une structure dans laquelle la recherche d'un élément ne nécessite pas de parcourir tous les éléments comme cela se passe dans une séquence chaînée.
Arbre binaire
L'exemple le plus simple est l'arbre binaire de recherche dans lequel tout nœud de l'arbre possède (généralement) un nœud fils gauche et un nœud fils droit et tels que les trois éléments de ces trois nœuds kitxmlcodeinlinelatexdvppfinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpgfinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpdfinkitxmlcodeinlinelatexdvp vérifient respectivement kitxmlcodeinlinelatexdvpg \le p < dfinkitxmlcodeinlinelatexdvp.
L'ensemble {3, 7, 13, 19, 23,25, 28} peut ainsi être représenté par l'arbre suivant :
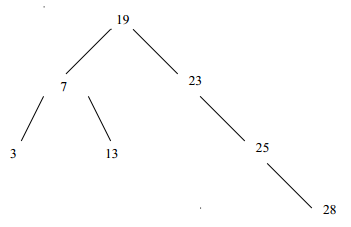
L'ensemble des opérations
|
appartient |
ensemble, ensemble |
→ booléen |
|
ajouter |
élément, ensemble |
→ ensemble |
|
enlever |
élément, ensemble |
→ ensemble |
admettent des algorithmes de complexité en temps proportionnel à la hauteur de l'arbre. Ces algorithmes seront étudiés dans le chapitre 6Chapitre 6 - Arbres binaires de recherche.
Des techniques relativement simples peuvent garantir qu'une hauteur d'arbre raisonnable, voire optimale, à savoir kitxmlcodeinlinelatexdvplog_2(n)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp est la cardinalité de l'ensemble. L'une de ces techniques est justement le fait des arbres rouges et noirs.
Tas : un exemple remarquable de limiter les primitives au strict minimum
Parfois le type ensemble utilisé est dégradé, c'est-à-dire défini à partir du type ensemble présenté plus haut en :
- supprimant une ou plusieurs opérations ;
- en restreignant l'utilisation d'une ou plusieurs opérations.
Par exemple, l'opération enlever peut consister uniquement à supprimer l'élément de plus grande valeur. Cet appauvrissement du type ensemble facilite fortement son implémentation. Une solution souvent retenue est l'utilisation d'arbres binaires appelés « tas » dans lequel l'élément d'un nœud est supérieur aux éléments des fils. Ainsi, l'élément minimal se trouve à la racine. Calculer l'élément maximal de l'ensemble consiste alors simplement à considérer l'élément se trouvant à la racine de l'arbre! Nous verrons comment supprimer cet élément ou ajouter tout nouvel élément en temps logarithmique.
Forêts
D'autres variantes du type ensemble existent. Par exemple une qui permet de manipuler une partition d'un ensemble donné en n'autorisant que les unions de ces parties. Les arbres sont une nouvelle fois utilisés et permettent (pour certains algorithmes) de réaliser l'union de deux parties à partir de deux de leurs éléments en temps (quasi) constant !
2. Chapitre 2 - Types abstraits▲
Intuitivement un type abstrait est un ensemble d'opérations pour lesquelles on définit une syntaxe et une sémantique. Plus formellement un type abstrait est la donnée :
- de sa signature décrivant la syntaxe du type, les noms des types utilisés pour sa définition) ainsi que le nom des opérations et le type de leurs arguments ;
- d'un ensemble d'axiomes définissant les propriétés des opérations.
La définition d'un tel ensemble d'axiomes est un exercice parfois délicat, car cet ensemble doit être à la fois :
- consistant c'est-à-dire les axiomes ne doivent pas être contradictoires ;
- complet, c'est-à-dire les axiomes sont suffisants pour décrire l'ensemble des propriétés du type abstrait.
Exemple 1
Ainsi, le type primitif booléen peut ainsi être défini :
|
Nom Booléen |
||
|
Opérations |
||
|
vrai |
: booléen |
→ booléen |
|
faux |
: booléen |
→ booléen |
|
¬ |
: booléen |
→ booléen |
|
∧ |
: booléen x booléen |
→ booléen |
|
∨ |
: booléen x booléen |
→ booléen |
Les axiomes sont :
- kitxmlcodeinlinelatexdvp\lnot(vrai())=faux()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\lnot(faux())=vrai()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\wedge(vrai(),vrai())=vrai()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\wedge(vrai(),faux())=faux()finkitxmlcodeinlinelatexdvp
- etc.
Lors de la définition d'un type abstrait, il est recommandé pour des raisons de simplicité de limiter le nombre d'opérations. Dans le cas présent, on démontre aisément que toute opération booléenne peut s'écrire sous forme normale disjonctive, c'est-à-dire sous la forme d'une disjonction (opérateur « OU ») de conjonctions (opérateur « ET » ) de littéraux positifs (variable simple) ou négatifs (variable précédée de l'opérateur kitxmlcodeinlinelatexdvp\lnotfinkitxmlcodeinlinelatexdvp). Par exemple, l'opération kitxmlcodeinlinelatexdvp\Rightarrowfinkitxmlcodeinlinelatexdvp se définit par kitxmlcodeinlinelatexdvpA \Rightarrow B := \lnot(A) \wedge Bfinkitxmlcodeinlinelatexdvp ; l'opération kitxmlcodeinlinelatexdvp\Leftrightarrowfinkitxmlcodeinlinelatexdvp se définit par kitxmlcodeinlinelatexdvpA \Leftrightarrow B := ((A) \wedge B) \vee (\lnot(A) \wedge \lnot(B))finkitxmlcodeinlinelatexdvp.
Remarque 1 Le plus célèbre des théorèmes en informatique est le théorème dit d'incomplétude de Godel qui indique qu'aucun ensemble fini d'axiomes n'est suffisant pour prouver l'ensemble des propriétés du type entier. Ainsi, formellement il est impossible de définir un type abstrait entier qui soit universel. Cependant, rassurez-vous. Le type entier ou tout autre type que vous serez amené à définir doit l'être dans le contexte de quelques algorithmes à écrire, dont la correction ou la terminaison nécessitent un nombre fini de propriétés sur ces entiers, et donc, d'un nombre fini d'axiomes.
2-1. Un exemple de type abstrait : le type ensemble▲
Définir un type abstrait est réalisé en fonction du contexte, c'est-à-dire en fonction du problème à résoudre, voire de l'algorithme le résolvant. Définir un type abstrait consiste à choisir un ensemble d'opérations. Réaliser un tel choix nécessite un arbitrage entre différents critères :
- Faire des choix conformes avec des définitions courantes ;
- Simplicité de la définition du type : que ce soit en ce qui concerne le nombre d'opérations, ou la définition des axiomes ;
- Simplicité de la définition de l'algorithme ;
- Optimisation de l'algorithme en ce qui concerne sa complexité en temps ou en espace.
2-1-1. Quelles opérations choisir ?▲
Considérons le type ensemble. Pour des raisons de simplicité, l'ensemble de ces opérations doit être minimal tout en étant suffisant pour permettre l'écriture de l'algorithme. Une définition universelle semblerait être :
|
Nom ensemble |
||
|
Utilise élément , booléen |
||
|
Opérations |
||
|
estVide |
: ensemble |
→ booléen |
|
ensembleVide |
: |
→ ensemble |
|
appartient |
: élément x ensemble |
→ booléen |
|
ajouter |
: élément x ensemble |
→ ensemble |
|
enlever |
: élément x ensemble |
→ ensemble |
|
choisir |
: ensemble |
→ élément |
Considérons un algorithme qui nécessite de calculer régulièrement la cardinalité d'un ensemble. Cette opération peut être définie à l'aide des opérations précédentes :
2.
3.
4.
5.
6.
fonction cardinalité(E:ensemble) :entier
i ← 0;
tantque ¬(estVide(E))
i ← i + 1;
E ← enlever(choisir(E),E);
retourner i;
Cependant, la complexité en temps de l'exécution de cette fonction (ici linéaire) peut s'avérer excessive alors que cette opération peut s'exécuter en temps constant par la simple présence dans la structure implémentant le type ensemble d'un entier indiquant sa cardinalité. Aussi, dans le cas où l'algorithme considéré requiert de calculer souvent la taille de l'ensemble ou, plus encore, si sa complexité en temps dépend de l'exécution de cardinalité en temps constant, il est préférable d'ajouter l'opération cardinalité : ensemble → entier dans la définition même du type.
2-1-2. Quels axiomes choisir ?▲
Que signifient les opérations suivantes ?
|
ajouter |
élément x ensemble |
→ ensemble |
|
enlever |
élément x ensemble |
→ ensemble |
Quatre significations s'offrent à nous selon que l'on accepte ou non l'exécution de l'opération ajouter sur un élément contenu dans l'ensemble et selon que l'on accepte ou non l'exécution de l'opération enlever sur un élément n'appartenant pas à l'ensemble.
Exemple 2 Supposons que nous souhaitions écrire un algorithme réalisant l'union de deux ensembles. Si l'opération ajouter peut s'exécuter sur un élément déjà présent dans l'ensemble, l'algorithme s'écrit simplement :
2.
3.
4.
5.
6.
fonction union1(A,B:ensemble) :ensemble
tantque ¬(estVide (B))
b ← choisir(B);
B ← enlever(b,B);
A ← ajouter(b,A);
retourner A;
Si l'opération ajouter ne peut pas s'exécuter sur un élément déjà présent dans l'ensemble, l'algorithme s'écrit simplement :
2.
3.
4.
5.
6.
7.
fonction union2(A,B:ensemble) :ensemble
tantque ¬(estVide(B))
b ← choisir(B);
B ← enlever(b,B);
si ¬(appartient(a,A)) alors
A ← ajouter(b,A);
retourner A;
Si l'on considère les deux critères que sont la simplicité de l'algorithme et sa complexité en temps, la préférence va à la première solution : le code est plus simple, la complexité en temps est au moins aussi bonne que la seconde.
Exemple 3 Supposons que l'on souhaite ne retenir d'un ensemble que les entiers pairs. Une solution à ce problème est :
2.
3.
4.
5.
6.
7.
8.
fonction impairs(A :ensemble) :ensemble
B ← ensVide();
tantque ¬(estVide(A)
a ← choisir(A);
A ← enlever(a,A);
si estPair(a) alors
B ← ajouter(a,B);
retourner B;
Ici, nous savons que tout élément candidat à être ajouté dans l'ensemble ne peut pas y appartenir. Nous avons donc tout intérêt à définir l'opération ajouter en interdisant l'ajout d'un élément déjà présent, et ce pour au moins deux raisons :
- En restreignant la puissance opératoire de ajouter, son implémentation peut être moins coûteuse en temps. Si l'ensemble est représenté par une liste sans répétition, l'ajout d'un élément non présent est fait en temps constant : on l'insère en première position. Par contre, l'ajout d'un élément éventuellement déjà présent nécessite de vérifier sa présence avant de l'y insérer ;
- En restreignant la puissance opératoire de ajouter, on détecte d'éventuelles erreurs dans l'écriture d'un exécutable. Vous pourrez demander lors de l'exécution de votre programme de vous signaler toute tentative d'ajouter un élément déjà présent et utiliser ce signal pour détecter une erreur soit dans le programme soit dans l'algorithme lui-même.
2-1-3. Écriture formelle des axiomes▲
Définir le sens des opérations est réalisé à l'aide d'axiomes, c'est-à-dire de formules logiques. Contrairement à une définition mathématique où l'on restreint la portée d'une fonction en restreignant les domaines des arguments, lors d'une définition axiomatique on restreint la portée d'une fonction en ne définissant le sens que pour des valeurs appartenant à des domaines précis.
Exemple 4 Considérons l'opération enlever que l'on autorise à opérer sur un élément h n'appartenant pas éventuellement à un ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp.
L'opération ensembliste mathématique sous-jacente est la fonction qui à tout ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et à tout élément kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp associe l'ensemble à kitxmlcodeinlinelatexdvpA \cup \{a\}finkitxmlcodeinlinelatexdvp.
Sa définition axiomatique est :
- kitxmlcodeinlinelatexdvp\forall a : element\ \forall b : element\ \forall A : ensemble\qquad appartient(a,ajouter(b,A)) = (a = b) \vee appartient(a,A)finkitxmlcodeinlinelatexdvp
Exemple 5 Considérons l'opération ajouter que l'on autorise à opérer sur un élément kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp appartenant nécessairement à un ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp.
L'opération ensembliste mathématique sous-jacente est la fonction qui à tout ensemble kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et à tout élément kitxmlcodeinlinelatexdvpa \notin Afinkitxmlcodeinlinelatexdvp associe l'ensemble noté kitxmlcodeinlinelatexdvpA \setminus afinkitxmlcodeinlinelatexdvp égal à kitxmlcodeinlinelatexdvpA - \{a\}finkitxmlcodeinlinelatexdvp.
Le mathématicien considèrera que l'expression kitxmlcodeinlinelatexdvp\{a\} \setminus afinkitxmlcodeinlinelatexdvp est incorrecte.
La définition axiomatique de enlever est :
-
kitxmlcodeinlinelatexdvp\forall a : element\ \forall b : element\ \forall A : ensemblefinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\lnot(appartient(b,A)) \Rightarrow ( appartient(a,ajouter(b,A)) = (a = b)\ \vee\ appartient(a,A) )finkitxmlcodeinlinelatexdvp
L'axiomatique garantit des propriétés dans la mesure ou les spécifications des fonctions ont été respectées : ici, on ne peut ajouter un élément à un ensemble qu'à la condition qu'il n'y appartienne pas. Si cette condition n'est pas respectée, l'algorithme peut s'exécuter, mais sa correction n'est pas garantie.
Par exemple, l'informaticien admettra éventuellement que l'algorithme suivant puisse s'exécuter :
2.
3.
4.
5.
6.
fonction test(): booléen
A ← ensembleVide();
A ← ajouter(1,A);
A ← ajouter(1,A);
A ← enlever(1,A);
retourner appartient(1,A);
Cependant, il ne garantira pas que le booléen évaluant l'expression appartient(1, A) soit faux !
Ceci n'est pas une coquetterie obscure. Démontrons qu'une implémentation correcte, naturelle et efficace du type ensemble a pour conséquence que test() retourne vrai.
Implémentons le type ensemble à l'aide d'une liste d'éléments sans répétition, et ce, sans se soucier de l'ordre des éléments. Une implémentation efficace de ajouter(a, A) est d'insérer a au premier rang de la liste (représentant) A. Une implémentation efficace de enlever(1, A) est de supprimer la première occurrence de 1 dans la liste A : puisqu'aucune répétition n'est admise dans la liste, il n'est pas utile de supprimer toutes les occurrences de 1, mais seulement la première.
Ainsi, lors de l'exécution de test l'ensemble A est successivement représenté par :
- ()
- (1)
- (1,1)
- (1)
Le booléen retourné par l'appel de test() est ainsi vrai.
2-2. Quelques types abstraits « séquence »▲
Il existe plusieurs façons de manipuler une séquence. Nous en présenterons cinq principales qui forment autant de types abstraits :
- le tableau ;
- la structure ;
- la pile ;
- la file ;
- la liste.
Cette liste n'est pas exhaustive. Vous serez parfois amené à en définir de nouvelles inspirées ou non de celles-ci. De même, vous serez parfois amené à enrichir l'une d'entre elles en ajoutant de nouvelles primitives.
2-2-1. Le tableau▲
Le premier type abstrait est le type tableau. Les opérations « tableau » permettent en fait de manipuler des séquences :
- dont les éléments sont de même type ;
- dont la taille est fixée à la création, on enrichit parfois le type tableau d'une ou plusieurs opérations permettant de modifier sa taille. Mais leurs utilisations doivent être rares. Si la longueur de la séquence doit souvent varier, il est souvent préférable de considérer une liste.
Signature
La signature du type tableau est la suivante :
|
Nom Tableau |
||
|
Utilise élément, entier |
||
|
Opérations |
||
|
tableau |
: entier x élément |
→ tableau |
|
taille |
: tableau |
→ entier |
|
lire |
: tableau x entier |
→ élément |
|
changer |
: tableau x entier x élément |
→ tableau |
La syntaxe étant peu pratique, nous en définirons une plus proche de celle utilisée dans différents langages de programmation. Ainsi,
- r ← t[4] permet d'associer à une variable r la valeur de l'élément se trouvant à l'indice 4 du tableau t. Cette écriture se substitue donc à l'instruction r ← lire(t,4) ;
- t[4] ← a permet de modifier la valeur de l'élément se trouvant à l'indice 4 du tableau t en lui attribuant la valeur de la variable a. Cette écriture se substitue donc à l'instruction t ← changer(t,4,a).
Axiomatique
Voici quelques axiomes définissant dans un langage logique l'ensemble des primitives :
- kitxmlcodeinlinelatexdvp\forall i \in \mathbb{N}\ \forall e : \acute{e}l\acute{e}ment\qquad taille (tableau[i] (e)) = ifinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall i \in \mathbb{N}\ \forall e : \acute{e}l\acute{e}ment\ \forall j \in [1,i]\qquad lire(tableau[i](e),j) = efinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall t : tableau\ \forall e : \acute{e}l\acute{e}ment\ \forall j \in [1, taille(t)]\ \forall k \in [1, taille(t)]\setminus j \qquad lire(changer(t,j,e),k) = lire(t,j,e)finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall t : tableau\ \forall e : \acute{e}l\acute{e}ment\ \forall j \in [1, taille(t)]\qquad lire(changer(t,j,e),j) = efinkitxmlcodeinlinelatexdvp
Exemples
La suite d'instructions suivantes :
2.
3.
t + tableau[5](0);
t[4] ← 10;
t[3] ← 2·[4];
a pour conséquence de créer un tableau d'entiers de taille 5 indicé de 1 à 5 dont la valeur est successivement :
2.
3.
4.
1 2 3 4 5
t = (0, 0, 0, 0, 0)
t = (0, 0, 0, 10, 0)
t = (0, 0, 20, 10, 0)
Remarque
Afin d'obtenir une définition simple cohérente du tableau avec celle de la liste, le premier indice d'un tableau t est l'entier 1. Ainsi le ie élément (son rang) est l'élément d'indice i.
Ce choix diffère de celui fait en langage C : le premier élément d'un tableau a pour indice 0. La raison est de pouvoir manipuler adresse et indice aisément : en C, l'adresse de t[i] n'est autre que la somme de t+i.
Si vous le souhaitez, il est possible d'enrichir le type tableau en définissant une opération tableau qui permet de choisir comme premier indice d'un tableau n'importe quel entier positif ou nul, voire n'importe quel entier relatif, voire n'importe quel caractère.
Remarque
Le terme tableau a souvent un autre sens : celui issu de langages de programmation tels que le langage C. En effet une implémentation très courante d'un tableau est d'utiliser un tableau, c'est-à-dire une zone mémoire où les éléments seront à des adresses correspondant à leur rang dans la séquence. Ainsi, en codant un entier sur 4 octets, la séquence-tableau (23, 12, 34, 56,3) sera codée sur 5 * 4 octets : si le premier élément 23 et à l'adresse 23002101, les éléments 12, 34, 56 et 3 seront aux adresses respectives 23002105, 23002109, 23002113 et 23002117.
La conséquence pratique de ce choix est pouvoir accéder à un élément à partir de son rang (ou indice) en temps constant. Ainsi, quand on évoque un tableau, on pense souvent à des opérations de lecture et d'écriture en temps constant.
2-2-2. La structure▲
Le second type abstrait « séquence » est le type structure. Les opérations « structurent » permettent en fait de manipuler des séquences :
- dont les éléments sont de types différents ;
- dont la taille est fixée à la création.
On dit qu'une structure est composée de champs qui ont chacun un nom et un type.
Signature
Soient n types abstraits E1,… , En, ainsi qu'un type « identifiant » Id, une définition du type structure peut être :
|
Nom structure |
||
|
Utilise Id, E1,… , En |
||
|
Opérations |
||
|
structure |
: Id x … x Id x E1… x En |
→ structure |
|
lire1 |
: structure |
→ E1 |
|
… |
||
|
liren |
: structure |
→ En |
|
changer1 |
: structure x E1 |
→ structure |
|
… |
||
|
changern |
: structure x En |
→ structure |
La syntaxe étant peu pratique, nous en définirons une autre. Ainsi :
- pour tout entier kitxmlcodeinlinelatexdvpi \in [1,n],\ a \leftarrow s,id_ifinkitxmlcodeinlinelatexdvp se substitue à kitxmlcodeinlinelatexdvpa \leftarrow lire_i(s)finkitxmlcodeinlinelatexdvp ;
- pour tout entier kitxmlcodeinlinelatexdvpi \in [1,n],\ s,id_i \leftarrow afinkitxmlcodeinlinelatexdvp se substitue à kitxmlcodeinlinelatexdvps \leftarrow changer_i(s,a)finkitxmlcodeinlinelatexdvp.
Axiomatique
Les axiomes du type structure sont laissés en exercice.
Exemples
La suite d'instructions suivantes :
t ← structure[abs,ord](1.0 , 2.0);
t.abs ← 3.0;
t.ord ← t.ord + t.abs;a pour conséquence de créer une structure t ayant deux champs d'identifiants abs et ord de types réels ; la structure est successivement égale à :
t = ( 1.0 , 2.0 )
t = ( 3.0 , 2.0 )
t = ( 3.0 , 5.0 )2-2-3. La pile▲
Une pile est une séquence dont toutes les opérations se font à une extrémité appelée la tête.
Signature
La signature du type pile est la suivante :
|
Nom pile |
||
|
Utilise élément |
||
|
Opérations |
||
|
estVide |
: pile |
→ booléen |
|
pileVide |
→ pile |
|
|
tête |
: pile |
→ élément |
|
empiler |
: pile x élément |
→ pile |
|
dépiler |
: pile |
→ pile |
Axiomatique
Voici quelques axiomes définissant dans un langage logique l'ensemble des primitives :
- kitxmlcodeinlinelatexdvpestVide(pileVide()) = vrai()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall p : pile\ \forall e : \acute{e}l\acute{e}ment\qquad estVide(empiler(p,e)) = fauxfinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall p : pile\ \forall e : \acute{e}l\acute{e}ment\qquad t\^ete(empiler(p,e)) = efinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall p : pile\ \forall e : \acute{e}l\acute{e}ment\qquad p = d\acute{e}piler(empiler(p,e))finkitxmlcodeinlinelatexdvp
Exemples
La suite d'instructions suivante :
2.
3.
4.
5.
6.
7.
8.
p ← empiler(pileVide(),10);
a ← tête(p);
p ← empiler(p,20);
b ← tête(p);
p ← empiler(p,30);
c ← tête(p);
p ← dépiler(p);
d ← tête(p);
a pour conséquence de créer une pile p et un entier a de valeurs successivement égales à :
2.
3.
4.
p = (10) a = 10
p = (20,10) b = 20
p = (30,20,10) c = 30
p = (20,10) d = 20
Remarques
En fonction des problèmes à résoudre ou des algorithmes à écrire, on peut ajouter ou remplacer des primitives par de nouvelles. À titre d'exemple, on peut supposer l'existence d'une opération fournissant la longueur de la séquence :
taille : pile → entierou une autre qui retire la tête de la pile :
extraireTête : pile → élément x piledont la définition algorithme pourrait simplement être :
fonction extraireTête(p:pile) : élément x pile
retourner(tête(p),dépiler(p))2-2-4. La file▲
Une file est une séquence dont toutes les opérations se font aux deux extrémités :
- la suppression et la lecture à la première extrémité ;
- l'ajout à la dernière extrémité.
Signature
La signature du type file est la suivante :
|
Nom file |
||
|
Utilise élément, booléen |
||
|
Opérations |
||
|
estVide |
: file |
→ booléen |
|
fileVide |
: |
→ file |
|
1erÉlément |
: file |
→ élément |
|
défiler |
: file |
→ file |
|
enfiler |
: file x élément |
→ file |
Axiomatique
Voici quelques axiomes définissant dans un langage logique l'ensemble des primitives :
- kitxmlcodeinlinelatexdvpestVide(fileVide()) = vrai() finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall e : \acute{e}l\acute{e}ment\qquad 1er\acute{E}l\acute{e}ment(enfiler(fileVide(),e)) = efinkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall e : \acute{e}l\acute{e}ment\qquad estVide(défiler(enfiler(fileVide(),e))) = vrai ()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall f : file\ \forall e : \acute{e}l\acute{e}ment\qquad non(estVide(f)) \Rightarrow d\acute{e}filer(enfiler(f,e)) = enfiler(d\acute{e}filer(f),e)finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall f : file\ \forall e : \acute{e}l\acute{e}ment\qquad estVide(enfiler(f,e)) = faux()finkitxmlcodeinlinelatexdvp
Exemples
La suite d'instructions suivante :
2.
3.
4.
5.
6.
7.
8.
f ← enfiler(fileVide(),10);
a ← 1erÉlément (f);
f ← enfiler(f,20);
b ← 1erÉlément (f);
f ← enfiler(f,30);
c ← 1erÉlément (f);
f ← défiler(f);
d ← 1erÉlément (f);
a pour conséquence de créer une file f et des entiers de valeurs successivement égales à :
2.
3.
4.
f = (10) a = 10
f = (10,20) b = 10
f = (10,20,30) c = 10
f = (20,30) d = 20
2-2-5. La liste▲
Une liste est une séquence munie d'opérations qui permettent d'accéder à chacun des éléments à partir de leur position (ici un rang) et qui modifient la séquence à partir d'insertion ou de suppression.
Signature
La signature du type liste est la suivante :
|
Nom liste |
||
|
Utilise élément, entier, booléen |
||
|
Opérations |
||
|
estListeVide |
: liste |
→ booléen |
|
listeVide |
: |
→ liste |
|
ièmeElmt |
: liste x entier |
→ élément |
|
insérer |
: élément x entier x liste |
→ liste |
|
supprimer |
: liste x entier |
→ liste |
|
longueur |
: liste |
→ entier |
Axiomatique
Voici quelques axiomes définissant dans un langage logique l'ensemble des primitives :
- kitxmlcodeinlinelatexdvpestListeVide(listeVide()) = vrai()finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall l : liste,\ \forall e : \acute{e}l\acute{e}ment,\ \forall i \in \mathbb{N}\\ \quad 1 \le i\le longueur(l)+1 \Rightarrow taille(ins\acute{e}rer(e,i,l)))= taille(l)+1finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall l : liste, \forall i \in \mathbb{N}\\ \quad 1\le i\le longueur(l) \Rightarrow taille(supprimer(i,l)))= taille(l)-1finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall l : liste,\ \forall e : \acute{e}l\acute{e}ment,\ \forall (i, j) \in \mathbb{N}^2\\ \quad 1\le j<i\le longueur(l)+1 \Rightarrow i\grave{e}meElmt(ins\acute{e}rer(e,i,l),j) = i\grave{e}meElmt(l, j) \\ \quad 1\le i=j\le longueur(l)+1 \Rightarrow i\grave{e}meElmt(ins\acute{e}rer(e,i,l),j) = e \\ \quad 1\le i<j\le longueur(l)+1 \Rightarrow i\grave{e}meElmt(ins\acute{e}rer(e,i,l),j) = i\grave{e}meElmt(l, j-1)finkitxmlcodeinlinelatexdvp
- kitxmlcodeinlinelatexdvp\forall l : liste,\ \forall (i, j) \in \mathbb{N}² \\ \quad 1\le j\le i\le longueur(l) \Rightarrow i\grave{e}meElmt(supprimer(i,l),j) = i\grave{e}meElmt(l, j) \\ \quad 1\le i\le j\le longueur(l)-1 \Rightarrow i\grave{e}meElmt(supprimer(i,l) ,j) = i\grave{e}meElmt(l, j+1)finkitxmlcodeinlinelatexdvp
Exemples
La suite d'instructions suivante :
2.
3.
4.
5.
6.
7.
l ← insérer(10,1,listeVide());
l ← insérer(20,2,l);
l ← insérer(30,3,l);
l ← insérer(40,2,l);
a ← ièmeElmt(l,1);
b ← ièmeElmt(l,2);
l ← supprimer(3,l);
a pour conséquence de créer une file l et des entiers de valeurs successivement égales à :
2.
3.
4.
5.
6.
7.
l = (10)
l = (10,20)
l = (10,20,30)
l = (10,40,20,30)
a = 10
b = 40
l = (10,40,30)
2-3. Conclusion▲
Nous avons présenté dans ce cours des types comme des ensembles d'opérations définies logiquement. Nous verrons dans le prochain chapitre comment les implémenter à l'aide de deux types le type tableau et le type structure qui sont fournis par la plupart des langages de programmation.
Cette approche logique ne suffit pas, si nous souhaitons étudier la complexité en temps des algorithmes, il nous faut définir un modèle de calcul réaliste qui garantisse un faible coût en temps des primitives considérées. Ce sera l'objet d'un prochain chapitre.
3. Chapitre 3 - Implémentations de types▲
Nous verrons ici quelques exemples d'implémentations d'objets.
3-1. Types primitifs et effets de bord▲
3-1-1. Types primitifs▲
Les types primitifs correspondent à des objets pouvant être codés sur des blocs mémoire de taille fixe. Ils permettent de représenter les quantités numériques que sont les booléens, les entiers, les rationnels, les réels. Conséquence de la taille fixe de leurs représentations en mémoire, toutes les opérations les concernant (∨, ≠, ∧, +, ·, log, sin, etc.) sont supposées être de complexité en temps constant.
Nous supposerons admise leur définition.
Insistons sur un point : tout type primitif est représenté à l'aide d'un nombre fixe d'octets. Ainsi, définir un type entier à l'aide d'un type primitif suppose que l'on se restreint à un nombre fini d'entiers (sur un octet l'ensemble d'entiers représentables est [0, 28-1], sur 4 octets il s'agit de [0, 24·8-1]). En conséquence de quoi, si vous souhaitez manipuler des entiers n de taille non arbitrairement fixée, il est nécessaire de les représenter à l'aide d'un type non primitif, par exemple une liste de longueur kitxmlcodeinlinelatexdvp\simeq \log_2(n)finkitxmlcodeinlinelatexdvp. Le coût des opérations ne pourra pas être considéré comme constant, mais dépendra alors de la longueur des listes.
Seront considérés comme non primitifs les types tableau, structure et tous les types construits à partir de ceux-ci notamment tous les types permettant de représenter des ensembles.
3-1-2. Effets de bord▲
Nous avons présenté des types permettant de manipuler des ensembles d'objets qu'ils soient ordonnés ou non (ensembles, séquences, et bientôt arbres). Ces ensembles nécessitent trivialement un espace mémoire de taille non constante (contrairement aux booléens, « petits » entiers et « petits » réels).
Nous avons défini pour ces objets de grande taille des opérations permettant de les modifier (par exemple dépiler pour la pile, ajouter pour l'ensemble, insérer pour une liste).
Une alternative s'offre à nous.
Opérations de complexité en temps faible, voire constant
Considérons l'exemple de l'opération dépiler du type pile et l'instruction : p ← dépiler(q);.
Il est possible de fournir une implémentation en temps constant (voir section prochaine). Or en temps constant, il est impossible de recopier l'espace mémoire utilisé par la pile q, éventuellement très grand ; en d'autres termes, la pile p utilise pour totalité ou presque totalité la zone mémoire de q et ce, quelle que soit l'implémentation d'une pile et de la fonction dépiler. En conséquence de quoi, une modification ultérieure de q entraînera sûrement une modification de p.
Il est par exemple possible qu'après exécution de p ← dépiler(p); les piles p et q soient égales, ou sinon aient les mêmes éléments.
Ceci remet en cause la définition axiomatique définissant les piles. Un choix à peine contraignant pour garantir les axiomes est de prendre pour membre droit d'une instruction uniquement la variable prise en argument et d'imposer ainsi comme seules instructions possibles :
q ← dépiler(q);Nous verrons que sous cette hypothèse dépiler(q) peut s'exécuter en temps constant. Ainsi, l'algorithme suivant qui cherche la présence d'un élément e dans une pile p
2.
3.
4.
5.
6.
7.
fonction appartient(e:élément; p : pile) : booléen
tantque non(estVide(p))
si tete(p)=e
retourner vrai();
p ← dépiler(p);
retourner faux();
a une complexité en temps kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp (avec n = taille(p)) et en espace kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp. Nous définirons dans le prochain chapitre un modèle de calcul complet et verrons dans cet exemple que la pile p après exécution de appartient(e,p) n'est pas modifiée.
Si vous souhaitez créer une nouvelle pile p obtenue en dépilant une pile q, il faut alors réaliser une copie préalable de q qui crée une pile ayant les mêmes éléments, mais utilisant une zone mémoire disjointe de celle utilisée par q. La complexité en temps de cette opération est bien sûr linéaire : c'est-à-dire proportionnelle au nombre d'octets nécessaire à la représentation de q. La suite d'instructions devient alors :
p ← dépiler(copie(q));Sous ces conditions, puisque les zones mémoire associées à p et q ne partagent aucun octet, aucune modification de p n'entraîne de modification de q et inversement.
Opérations de complexité en temps linéaire
Une autre solution consisterait lorsque l'on définit l'opération dépiler de systématiquement réaliser une copie de l'ensemble (ici une pile) passé en argument. Cela aurait l'avantage de pouvoir exécuter l'instruction
p ← dépiler(copie(q));sans craindre qu'une modification ultérieure de p ne modifie q (et inversement).
L'intérêt est logique : les axiomes sont garantis. Mais l'utilité de par exemple dépiler est réduit.
Ainsi, l'algorithme suivant qui cherche la présence d'un élément e dans une pile p
2.
3.
4.
5.
6.
7.
fonction appartient(e:élément; p : pile) : booléen
tantque non(estVide(p))
si tete(p)=e
retourner vrai();
p ← dépiler(p);
retourner faux();
a une complexité en temps kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp (avec n = taille(p)) et en espace kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp.
3-2. Tableau infini▲
En introduction de ce cours, nous avons vu comment l'objet « séquence » pouvait être représenté en mémoire selon une zone mémoire contiguë qui permet l'accès à un élément selon son rang en temps constant ou selon un chaînage avec un accès en temps non constant.
Contrairement au principe qui souhaite ne pas mélanger la définition du type abstrait de son implémentation, les usages courants en algorithmique font que tout type abstrait « tableau » désigne un type séquence implémenté selon une zone contiguë.
Un exemple fameux de type tableau est tableauInfini dont la signature est :
|
Nom tableaulnfini |
||
|
Utilise entier, élément |
||
|
Opérations |
||
|
tableaulnfini |
: élément |
→ tableaulnfini |
|
ième |
: tableaulnfini x entier |
→ élément |
|
changerIème |
: tableaulnfini x entier x élément |
→ tableaulnfini |
Définir un tableau infini est fait simplement à l'aide d'une structure contenant deux champs :
- Un premier champ de nom tab de type tableau ;
- Un second champ de nom val contenant la valeur de type élément apparaissant une infinité de fois.
La figure 3.1 fournit une définition du constructeur tableauInfini.
2.
3.
fonction tableaulnfini(e: élément) : structure
t ← tableau[e](100);
retourner structure(tab,val)(t,e);
La définition de ième ne pose aucune difficulté :
2.
3.
4.
5.
fonction ième(t:tableaulnfini , i: entier): élément
si i ≤ taille(t.tab) alors
retourner t.tab[i];
sinon
retourner t.val;
Voici une implémentation de changerIème :
2.
3.
4.
fonction changerIème(t:tableaulnfini,i:entier,e:élément):tableaulnfini
t ← extensionÉventuelle(t,i);
t.tab[i] ← e;
retourner t;
où extensionEventuelle est ainsi défini :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
fonction extensionÉventuelle(t:tableaulnfini,i:entier) :tableaulnfini
si i ≤ taille(t.tab)
retourner t;
sinon
ntaille ← stratégieExtension(taille(t.tab),i);
u ← tableau(ntaille)(t.val);
pour i + 1 à taille(t.tab)
u[i] ← t.tab[i];
t.tab ← u;
retourner t;
Dès que l'on souhaite modifier la valeur d'un élément se trouvant au-delà du tableau fini tab, on étend ce tableau à une taille au moins égale à cet indice. Trois stratégies définies par la fonction stratégieExtension se présentent alors :
-
Soit on fait du juste mesure. On étend le tableau exactement de ce dont on a besoin. Plus formellement nous avons :
Sélectionnezfonction stratégieExtension(n:entier,i:entier):entier retourner i; -
On peut affiner cette méthode en l'étendant à l'indice désiré, mais à l'indice immédiatement supérieur multiple d'une constante fixée, par exemple égale à 100. Plus formellement nous avons :
Sélectionnezfonction stratégieExtension(n:entier,i:entier):entier retourner ⌈ i/100 ⌉; - Soit on anticipe des besoins futurs de façon à limiter le nombre de telles extensions. Une stratégie efficace consiste à systématiquement doubler la taille du tableau. Plus formellement nous avons :
2.
3.
4.
5.
6.
7.
8.
fonction stratégieExtension(n:entier,i:entier):entier
nt ← n;
faire
nt ← nt · 2;
jusqu'à nt ≥ i
retourner nt;
Exemple 6 Ainsi l'algorithme :
2.
3.
t ← tableaulnfini(0);
pour i de 1 à n
t ← changerIème(t,i,i·2);
réalisera
- n extensions selon la première stratégie. La complexité en temps cumulée est kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp. Ceci est toujours extrêmement coûteux. Cette stratégie doit être abandonnée ;
- n/100 extensions selon la seconde (dans le cas où la constante est 100). La complexité en temps cumulée est kitxmlcodeinlinelatexdvpO\left (\frac{n}{100}^2\right)finkitxmlcodeinlinelatexdvp. Cette stratégie est théoriquement identique à la première, mais peut être employée dans certains algorithmes ;
- kitxmlcodeinlinelatexdvp\log_2(n)finkitxmlcodeinlinelatexdvp extensions selon la troisième. La complexité en temps cumulée est kitxmlcodeinlinelatexdvpO(2\cdot n)finkitxmlcodeinlinelatexdvp, c
- ar égale à kitxmlcodeinlinelatexdvpO(1 + 2 + 2^2 + \dots + 2^{\log_2(n)})finkitxmlcodeinlinelatexdvp. Cette stratégie est pour cette raison préférable aux deux précédentes.
3-3. Représentation d'une pile par une zone mémoire contiguë▲
Une utilisation immédiate d'un tableau infini est l'implémentation d'une pile.
|
Nom pile |
||
|
Utilise élément |
||
|
Opérations |
||
|
pileVide |
: |
→ pile |
|
estVide |
: pile |
→ booléen |
|
empiler |
: pile x élément |
→ pile |
|
dépiler |
: pile |
→ pile |
|
tête |
: pile |
→ élément |
Et ce, sous la forme d'une structure ayant deux champs, ce tableau ainsi que l'indice de l'élément au sommet de la pile, l'indice étant égal à 0 si la pile est vide.
2.
3.
4.
5.
6.
7.
8.
fonction pileVide() :pileRéel
t ← tableauInfini(0.0);
retourner structure(tab,ind)(t,0);
fonction empiler(p:pileRéel, r:réel):pileRéel
p.ind ← p.ind + 1;
p.tab ← changerIème(p.tab,p.ind,r);
retourner p;
Exercice 1 Écrire les autres primitives.
Remarque 2 Conformément au modèle présenté lors du dernier chapitre, les piles sont des types non primitifs. Ainsi, l'algorithme
2.
3.
4.
5.
fonction test () :booléen
p ← pileVide();
q ← p;
q ← empiler(q, 1.5);
retourner (estVide(q));
retourne faux.
En effet, les objets de types non primitifs p et q partagent toujours la même référence donc désignent toujours le même objet égal à la fin à la pile contenant l'unique réel 1.5 : l'affectation q ← p; qui fait en sorte que les deux objets de types non primitifs p et q partagent la même référence, donc désignent le même objet, l'instruction suivante q ← empiler(q, 1.5); ne modifie pas la référence de q qui reste donc égale à celle de p.
Remarque 3 Si l'on souhaite à partir d'une pile p définir une pile q ayant les mêmes éléments, mais dont aucune modification sur p n'entraîne de modification sur q, il nous faut nécessairement réaliser une « copie » de la première, et ce, dans une zone mémoire disjointe de la seconde.
Exercice 2 Écrire une telle fonction copie.
3-4. Représentation d'une liste itérative à l'aide d'un chaînage▲
Une définition du type abstrait liste est la suivante :
|
Nom liste |
||
|
Utilise élément, entier |
||
|
Opérations |
||
|
estListeVide |
: liste |
→ booléen |
|
listeVide |
: |
→ liste |
|
ièmeElmt |
: liste x entier |
→ élément |
|
insérer |
: élément x entier x liste |
→ liste |
|
supprimer |
: entier x liste |
→ liste |
|
longueur |
: liste |
→ entier |
3-4-1. Encapsulation du type élément dans un nœud▲
Une première idée qui sera réutilisée dans le cas d'objets plus complexes, tels les arbres, est de définir un nouveau type abstrait, le type nœud, qui encapsule le type élément. Cette définition complexifie la définition du type liste en nécessitant de définir le nouveau type abstrait nœud. Ce coût initial est largement compensé par la simplicité des algorithmes implémentant les différentes primitives comme nous le verrons plus loin. Voici la signature d'un tel type :
|
Nom nœud |
||
|
Utilise élément, booléen |
||
|
Opérations |
||
|
constructNœud |
: élément x nœud |
→ nœud |
|
?suivant |
: nœud |
→ booléen |
|
suivant |
: nœud |
→ nœud |
|
contenu |
: nœud |
→ élément |
|
changerCont |
: nœud x élément |
→ nœud |
|
changerSuiv |
: nœud X nœud |
→ nœud |
L'implémentation d'un tel objet est réalisée à l'aide d'une structure contenant deux champs :
- Un champ de nom cont de type élément ;
- Un champ de nom suiv désignant le nœud suivant.
Voici l'écriture de quelques primitives :
2.
3.
4.
5.
6.
fonction constructNœud(e :élément, n:nœud) :nœud
retourner structure(cont,suiv)(e,n);
fonction changerSuiv(n:nœud,p:nœud) :nœud
n.suiv ← p;
retourner n;
3-4-2. Sentinelle avant▲
Si l'on souhaite insérer un élément e en ie position, deux cas apparaissent selon que i est égal à 1 ou non :
- si i = 1, le nouveau premier nœud est celui contenant cet élément e ;
- si i ≠ 1, le premier nœud est inchangé.
Cette singularité i= 1 complexifie cet algorithme. Il est facile de se douter que d'autres algorithmes le seront aussi.
Une seconde idée permet de simplifier l'écriture de nombreux algorithmes. Elle consiste à utiliser une « sentinelle avant » : l'idée étant de représenter en mémoire la liste (3,5) par une liste composée de trois éléments (#,3,5), la valeur du premier élément n'ayant aucune importance quant à la valeur de la liste représentée : cet élément s'appelle la sentinelle avant.
Ainsi, une liste sera représentée par un type structure contenant un unique champ de nom sentinelleAvant et désignant cette sentinelle avant.
Pour des raisons similaires, il est souhaitable de rajouter une sentinelle arrière.
Supposons donc enrichi le type nœud de façon à pouvoir produire des nœuds sentinelles et à pouvoir tester si un nœud est une sentinelle. En d'autres termes, supposons les opérations :
|
sentinelle |
: |
→ nœud |
|
?sentinelle |
: nœud |
→ booléen |
Ainsi, la fonction listeVide peut se définir comme suit :
2.
3.
4.
fonction listeVide():liste
n ← sentinelle();
n ← changerSuivant(n,sentinelle());
retourner structure (sentinelleAvant)(n);
Une fonction très utile de nom ièmeNœud permet à partir d'une liste et d'un entier i de retourner son ie nœud (le nœud sentinelle si i = 0). La fonction ièmeNœud peut ainsi être définie :
2.
3.
4.
5.
6.
7.
fonction ièmeNœud(l:liste; i:entier) :nœud
n ← l.sentinelleAvant;
pour i ← 1 à i faire
n ← suivant(n);
retourner n;
Il en découle les définitions des primitives ième et insérer (Figures 3.2 et 3.3).
2.
fonction ième(l:liste;i:entier) :élément
retourner contenu(ièmeNœud(l,i));
2.
3.
4.
5.
6.
fonction insérer(l:liste,i:entier,e:élément):liste
prec ← ièmeNœud(l,i-1);
n ← constructNœud[e,suivant(prec)](cont, suiv);
prec ← changerSuiv(prec,n);
retourner l;
Exercice 3 Écrire la fonction supprimer.
Exercice 4 Indiquer comment singulariser un nœud comme nœud sentinelle.
En d'autres termes, écrire les primitives sentinelle et ?sentinelle.
3-4-3. Autre attribut de la liste : sa longueur▲
Si l'algorithme le requiert, pour simplifier ou optimiser l'algorithme nous pouvons définir de nouveaux attributs au type liste.
Nous pouvons par exemple implémenter le type liste de façon à ce que le calcul de la longueur se fasse en temps constant.
Pour cela :
- Nous enrichissons le type abstrait de la fonction : longueur liste → entier ;
- Nous ajoutons dans la structure implémentant la liste un champ longueur initialisé à 0 et modifié lors de toute modification de la liste.
La fonction listeVide peut se définir ainsi :
2.
3.
4.
5.
fonction listeVide() liste
n ← sentinelle();
n ← changerSuivant(a,sentinelle());
retourner structure(sentinelleAvant,longueur)(n,0);
Exercice 5 Écrire les autres primitives du type liste.
3-4-4. Un autre attribut de la liste : le curseur▲
L'exécution de la fonction test de la Figure 3.4 double la valeur de chaque élément entier d'une liste l ; il a une complexité en temps en kitxmlcodeinlinelatexdvpO(longueur(l)^2)finkitxmlcodeinlinelatexdvp, puisque l'exécution de ièmeNœud(l,i) est égale à kitxmlcodeinlinelatexdvpO(i)finkitxmlcodeinlinelatexdvp.
2.
3.
4.
5.
6.
7.
8.
fonction test(l:liste) : liste
n ← taille(l);
pour i ← 1 à n
p ← ièmeNœud(l,i);
p ← changerCont(p,2·contenu(p));
retourner l;
Certes, on aurait pu réécrire l'algorithme en parcourant les nœuds de proche en proche et obtenir un algorithme linéaire. Mais nous allons montrer qu'une meilleure implémentation permet d'obtenir une complexité en temps linéaire sans modifier l'algorithme.
Cette idée consiste à ajouter à l'implémentation de la liste un nœud curseur (nom du champ curseur) ainsi que son rang (nom du champ rangCurseur). Ce curseur est positionné sur le ie nœud à chaque appel de la fonction ièmeNœud.
Ainsi, si le curseur est le nœud de rang i (le ie nœud) d'une liste l, la complexité en temps de l'exécution de ièmeNœud sur l'entrée l et i+1 (voire i, i+2) est constant et non plus kitxmlcodeinlinelatexdvpO(i+1)finkitxmlcodeinlinelatexdvp.
L'écriture de ièmeNœud est alors :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
fonction ièmeNœud(l:liste;i:entier) :nœud
si l.rangCurseur ≤ i
n ← n.curseur;
j ← n.rangCurseur;
sinon
n ← l.sentinelleAvant;
j ← 0;
tantque j < i faire
n ← suivant(n);
j ← j + 1;
l.curseur ← n;
l.rangCurseur ← i;
retourner n;
En conséquence de quoi, il est facile d'observer que la fonction test de la Figure 3.4 a une complexité en temps égale non pas à kitxmlcodeinlinelatexdvpO(longueur(l)^2)finkitxmlcodeinlinelatexdvp mais kitxmlcodeinlinelatexdvpO(longueur(l))finkitxmlcodeinlinelatexdvp.
Exercice 6 Écrire les autres primitives du type liste selon que le type nœud présente un simple ou un double chaînage.
3-4-5. Implémentation du type liste▲
Implémenter le type liste se fait en utilisant un type structure composé des champs :
- s ;
- c ;
- rangC ;
- longueur.
Les différentes fonctions se définissent ainsi :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
fonction estVide(l : liste) : booléen
retourner l.longueur = 0;
fonction longueur(l : liste) : entier
retourner l.longueur;
fonction listeVide() : liste
n ← sentinelle();
n ← changerSuivant(a,sentinelle());
retourner structure(sentinelleAvant,curseur,indiceCurseur, longueur)
(n, n, 0, 0);
fonction ièmeElmt(l : liste; i : entier) : élément
retourner contenu(ièmeNœud(1, i))
fonction supprimer(l : liste; i : entier) : liste
n ← ièmeNœud(l,i-1);
n ← changerSuivant(n,suivant(n));
retourner l;
fonction insérer(e : élément; i : entier; l : liste ) : liste
n ← ièmeNœud(l,i-1);
ajout ← constructNœud(e,suivant(n));
n ← changerSuiv(n,ajout);
retourner l;
3-4-6. Implémentation d'un nouveau type liste▲
Il est possible de repenser totalement la définition du type abstrait, c'est-à-dire du nombre et du sens de chacune des opérations en fonction des concepts introduits. Ceci permet d'écrire des algorithmes en utilisant des routines de bas niveau manipulant ici par exemple des curseurs et permettant d'évaluer très précisément la complexité de ces algorithmes.
Voici, un exemple de nouvelle signature :
|
Nom nouvelleListe |
||
|
Utilise nœud, entier, booléen |
||
|
Opérations |
||
|
estVide |
: nouvelleListe |
→ booléen |
|
listeVide |
: nouvelleListe |
→ nouvelleListe |
|
curseur |
: nouvelleListe |
→ nouvelleListe |
|
rangCurseur |
: nouvelleListe |
→ entier |
|
debut |
: nouvelleListe |
→ nouvelleListe |
|
fin |
: nouvelleListe |
→ nouvelleListe |
|
avant |
: nouvelleListe |
→ nouvelleListe |
|
tropADroite |
: nouvelleListe |
→ booléen |
où la signification des opérations est ainsi « vulgairement » définie :
- début (fin) positionne le curseur sur le premier (resp. dernier) nœud ;
- avant avance le curseur ;
- tropADroite indique si le curseur a débordé de la dernière position.
Exercice 7 Définir un type nœud permettant d'implémenter en temps constant une opération arrière:liste → liste qui permet de reculer le curseur.
Remarque
La liste d'opérations définissant le type nouvelleListe est fournie à titre d'exemple. On peut la modifier en ajoutant par exemple des opérations du type liste comme ièmeElmt, de nouvelles opérations comme ièmeNœud, avancerIèmeRang etc. Il est inutile de vouloir définir un type liste universel, car le nombre d'opérations serait trop élevé. Le choix de ces opérations est dicté par le problème à résoudre et l'algorithme à écrire.
3-5. Conclusion▲
Nous avons présenté quelques principales améliorations possibles au type abstrait ou à son implémentation. Une amélioration parfois utile est de pouvoir parcourir la liste dans les deux sens.
Cela se fait simplement en enrichissant le type nœud en permettant l'accès au nœud précédent par ajout des fonctions :
|
?prec |
: nœud |
→ booléen |
|
preced |
: nœud |
→ nœud |
|
changerPrec |
: nœud x nœud |
→ nœud |
et d'ajouter dans la structure un nouveau champ prec.
Cette liste d'amélioration n'est pas exhaustive. Vu leur nombre, il est fastidieux d'intégrer toutes les fonctionnalités dans un même type. Le choix des fonctions accessibles et de leur implémentation doit être réalisé en fonction du problème à résoudre et de l'algorithme à écrire.
4. Chapitre 4 - Arbres binaires▲
Une façon très courante de représenter un ensemble est d'utiliser non une séquence, mais une arborescence, c'est-à-dire une structure bidimensionnelle accessible à partir d'un premier élément appelé la racine et qui permet d'accéder de façon récursive de père en fils à chacun des éléments d'une unique façon.
Cette structure récursive permet d'implémenter les ensembles en obtenant des primitives de complexité très faible (en temps logarithmique).
Afin de simplifier, nous nous intéresserons à une sous-classe des arborescences, les arbres binaires.
4-1. Définition▲
Une définition simple d'un arbre binaire est sa définition récursive :
Définition 1 (Arbre binaire) Un arbre binaire T est :
soit l'arbre vide, noté kitxmlcodeinlinelatexdvp\emptysetfinkitxmlcodeinlinelatexdvp ;
soit un triplet (r, g, d) où :
- r est un nœud, appelé la racine de T, noté rac(T),
- g est un arbre binaire, appelé le sous-arbre gauche de T, noté ga(T),
- d est un arbre binaire, appelé le sous-arbre droit de T, noté dr(T).
Définition 2 (Père, frère…) La racine d'un arbre T est le père de la racine du sous-arbre gauche (resp. droit) si celle-ci existe. Deux nœuds ayant même père sont déclarés frères. L'ascendant d'un nœud est son père ou un ascendant de celui-ci. La distance d'une racine à un nœud est le nombre d'ascendants de ce dernier. Une feuille est un nœud sans fils.
Définition 3 (Hauteur) La hauteur d'un arbre est la plus grande distance d'un nœud à la racine : un arbre ayant pour unique sommet sa racine est de hauteur nulle.
Un premier type abstrait découlant de cette définition est le suivant :
|
Nom Arbre |
||
|
Utilise élément, entier, booléen |
||
|
Opérations |
||
|
estVide |
: Arbre |
→ booléen |
|
arbreVide |
: |
→ Arbre |
|
arbreGauche |
: Arbre |
→ Arbre |
|
arbreDroit |
: Arbre |
→ Arbre |
|
racine |
: Arbre |
→ élément |
|
consArbre |
: élément x Arbre x Arbre |
→ Arbre |
Ce premier type abstrait a l'avantage de sa simplicité, il pourra donc être utilisé dans certaines premières définitions d'algorithme. Mais, si l'on souhaite écrire des algorithmes avancés et évaluer leur complexité en temps et en espace, il souffre des mêmes limites rencontrées par le type abstrait liste à l'opposé de nouvelleListe.
4-2. Arbre binaire parfait▲
Définition 4 Un arbre binaire de hauteur est parfait s'il est complètement rempli sur tous les niveaux, sauf parfois, le plus bas qui est rempli en partant de la gauche jusqu'à un certain point.
Supposons que nous ayons à implémenter des arbres binaires parfaits. Une solution serait de considérer n'importe quelle implémentation d'arbre binaire : qui peut le plus peut le moins. Ceci peut être une erreur, car cette implémentation ne bénéficierait pas des singularités d'un arbre parfait.
Les seules modifications autorisées d'un arbre binaire parfait sont ou de modifier le contenu d'un nœud, ou de supprimer le dernier nœud (le plus à droite sur le dernier niveau) ou d'ajouter un nœud à la « suite » du dernier le plus à droite sur le dernier niveau (ou si celui-ci est rempli) d'en ajouter un le plus à gauche sur le nouveau dernier niveau.
Une implémentation consiste à utiliser un tableau dont la taille est égale à la taille n de l'arbre (c'est-à-dire son nombre de nœuds) ayant pour ensemble d'indices [1,n] de telle sorte que :
- Le nœud racine est l'indice 1 ;
- Le nœud fils gauche d'un nœud i est 2 · i ;
- Le nœud fils droit d'un nœud i est 2 · i + 1.
Exemple 7 Ainsi l'arbre binaire parfait suivant :
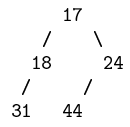
a pour représentation le tableau suivant :
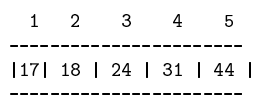
On observe que le nœud d'élément 24 a pour fils gauche le nœud d'élément 45 ; leur indice respectif dans le tableau est 3 et 6 et vérifie : 3cot 2 = 6.
4-3. Implémentation chaînée d'un arbre binaire▲
Pour les mêmes raisons qui nous ont amené à définir une liste comme une séquence de nœuds mutuellement chaînés, nous définissons un arbre comme un ensemble de nœuds mutuellement chaînés.
Les définitions que nous présentons ici ne sont pas universelles, elles peuvent évoluer selon le problème à résoudre ou l'algorithme à écrire. À l'image du type nouvelleListe, la définition du type arbre repose sur la définition du type abstrait nœud.
|
Nom arbre |
||
|
Utilise nœud, entier, booléen |
||
|
Opérations |
||
|
estVide |
: arbre |
→ booléen |
|
arbreVide |
: |
→ arbre |
|
racine |
: arbre |
→ nœud |
|
prendreRacine |
: nœud |
→ arbre |
Une définition du type nœud peut être la suivante :
|
Nom nœud |
||
|
Utilise élément, booléen |
||
|
Opérations |
||
|
contenu |
: nœud |
→ élément |
|
?filsGauche |
: nœud |
→ booléen |
|
?filsDroit |
: nœud |
→ booléen |
|
filsGauche |
: nœud |
→ nœud |
|
filsDroit |
: nœud |
→ nœud |
|
estSentinelle |
: nœud |
→ booléen |
|
constructSentinelle |
: |
→ nœud |
|
constructNœud |
: élément x nœud x nœud |
→ nœud |
|
changerFilsGauche |
: nœud x nœud |
→ nœud |
|
changerFilsDroit |
: nœud x nœud |
→ nœud |
|
changerContenu |
: nœud x élément |
→ nœud |
Afin de rendre plus lisibles les algorithmes en définissant de nouvelles opérations obtenues en dégradant l'opération constructNœud. Voici de nouvelles opérations possibles :
|
Utilise élément, booléen |
||
|
Opérations(suite) |
||
|
changerFilsGauche |
: nœud x nœud |
→ nœud |
|
changerFilsDroit |
: nœud x nœud |
→ nœud |
|
changerContenu |
: nœud x élément |
→ nœud |
Le type défini ici ne permet en fait que de parcourir l'arbre de haut en bas (de la racine vers les feuilles). On peut souhaiter pouvoir accéder à partir d'un nœud à son père. Il nous faut alors rajouter les opérations suivantes :
|
Utilise booléen |
||
|
Opérations(suite) |
||
|
?père |
: nœud |
→ booléen |
|
père |
: nœud |
→ nœud |
|
changerPère |
: nœud x nœud |
→ nœud |
et modifier bien sûr en conséquence le constructeur nœud constructNœud dont la nouvelle signature doit être :
|
constructNœud |
: élément x nœud x nœud x nœud |
→ nœud |
4-3-1. Définitions des primitives▲
Un arbre peut ainsi être défini à l'aide d'une structure composée d'un unique champ :
- de nom racine de type nœud.
Ce qui fournit la primitive suivante :
fonction racine(t : arbre) : nœud
retourner t.racine;Dans le cas singulier de l'arbre vide (qui ne contient ni nœud, ni racine), une représentation simple est de le représenter à l'aide d'un nœud qui est une sentinelle :
2.
3.
4.
5.
6.
7.
8.
9.
fonction arbreVide() : arbre
n ← constructSentinelle();
retourner structure(racine)(n);
fonction estVide(t : arbre) : booléen
retourner estSentinelle(t.racine);
fonction prendreRacine(n : nœud) : arbre
retourner structure(racine)(n);
Un nœud peut être défini à l'aide d'une structure composée de cinq champs :
- un champ de nom cont de type élément ;
- trois champs de noms gauche, droit, père de type nœud ;
- un champ de nom sent de type booléen indiquant si c'est une sentinelle.
Il en découle les définitions suivantes :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
fonction constructNœud(e : élément; g,d,p : nœud ) : nœud
retourner structure(cont,gauche,droit,père,sent)(e,g,d,p,faux());
fonction constructSentinelle() : nœud
retourner structure(cont,gauche,droit,père,sent)(0,0,0,0,vrai());
fonction estSentinelle(n : nœud) : booléen
retourner n.sent;
fonction ?filsGauche(n : nœud) : booléen
retourner estSentinelle(filsGauche);
fonction changerFilsDroit(n,droit : nœud) : nœud
n.droit ← droit;
retourner n;
5. Chapitre 5 - Parcours d'arbres▲
Un parcours d'arbres est un algorithme qui permet de visiter chacun des nœuds de cet arbre. Il existe plusieurs façons de les parcourir. Nous en présentons ici deux. Ces techniques concernent en fait tous les arbres. En vue de simplifier cet exposé, nous les présenterons sur des arbres binaires.
La première est familière à une définition récursive de l'arbre. Il s'agit du parcours en « profondeur » qui consiste à définir le parcours d'un arbre comme le parcours de son sous-arbre gauche augmenté du parcours de son sous-arbre droit. Ce parcours défini ici récursivement admet une écriture algorithmique équivalente itérative utilisant une Pile.
La seconde consiste à parcourir les nœuds de l'arbre en traitant prioritairement les nœuds les plus proches de la racine. Ce parcours est appelé parcours en largeur. Nous verrons comment écrire itérativement un tel parcours à l'aide d'une file.
5-1. Parcours en profondeur▲
L'algorithme de parcours en profondeur est défini en utilisant une fonction
2.
3.
procédure parcoursArbreProfondeur(T:arbre)
si non(estVide(T))
parcoursProfondeur(racine(T));
auxiliaire parcourant récursivement les nœuds parcoursProfondeur (Figure 5.1).
L'algorithmique est générique et utilise trois fonctions auxiliaires traiter1, traiter2, traiter3. Afin de simplifier l'exposé, nous pouvons supposer que ces opérations ne réalisent pas de modifications de la structure de l'arbre et ne réalisent qu'un calcul local au nœud traité (éventuellement, elles ne font rien).
2.
3.
4.
5.
6.
7.
8.
9.
procédure parcoursProfondeur (n :nœud)
si estSentinelle(n) alors
traiter4(n);
sinon
traiter1(n);
parcoursProfondeur(filsGauche(n));
traiter2(n);
parcoursProfondeur(filsDroit(n));
traiter3(n);
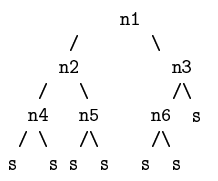
Exemple 8 Sur l'exemple de l'arbre binaire de la Figure 5.2 (les sentinelles sont indifféremment nommées s) l'exécution de l'algorithme entraîne l'exécution des instructions suivantes :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
traiter1(n1); traiter1(n2); traiter1(n4); traiter4(s);
traiter2(n4); traiter4(s);
traiter3(n4);
traiter2(n2);
traiter1(n5); traiter4(s);
traiter2(n5); traiter4(s);
traiter3(n5); traiter3(n2);
traiter2(n1);
traiter1(n3); traiter1(n6); traiter4(s);
traiter2(n6); traiter4(s);
traiter3(n6);
traiter2(n3); traiter4(s);
traiter3(n3); traiter3(n1);
5-1-1. Parcours préfixe, infixe ou suffixe▲
Il arrive parfois que le problème à résoudre nécessite un unique traitement sur chacun des nœuds (deux des trois traitements traiter1, traiter2, traiter3 consistent à ne rien faire). Nous parlons alors de parcours :
- préfixe si traiter2 et traiter3 sont des instructions vides ;
- infixe si traiter1 et traiter3 sont des instructions vides ;
- suffixe si traiter1 et traiter2 sont des instructions vides.
Exemple 9 Sur l'exemple de l'arbre précèdent, le parcours préfixe consistant à n'exécuter que les instructions traiter1 provoque l'exécution de :
2.
3.
traiter1(n1); traiter1(n2); traiter1(n4);
traiter1(n5);
traiter1(n3); traiter1(n6);
Exemple 10 Sur l'exemple de l'arbre précédent, le parcours infixe consistant à n'exécuter que les instructions traiter1 provoque l'exécution de :
2.
3.
4.
5.
6.
traiter2(n4);
traiter2(n2);
traiter2(n5);
traiter2(n1);
traiter2(n6);
traiter2(n3);
Exemple 11 Sur l'exemple de l'arbre précédent, le parcours postfixe consistant à n'exécuter que les instructions traiter1 provoque l'exécution de :
2.
3.
4.
traiter3(n4);
traiter3(n5); traiter3(n2);
traiter3(n6);
traiter3(n3); traiter3(n1);
Exemple 12 Si nous souhaitons placer dans une file les contenus des différents nœuds en utilisant un parcours préfixe, l'algorithme de parcours s'écrit ainsi :
2.
fonction parcoursArbre1(T:arbre) : file
retourner parcours1(racine(T),fileVide());
où parcours1 est défini par la Figure 5.3.
2.
3.
4.
5.
6.
7.
fonction parcoursi(n:nœud,F:file) file
si non(estSentinelle(n)) alors
F ← enfiler(contenu(n),F);
F ← parcoursi(filsGauche(n),F);
F ← parcoursi(filsDroit(n),F);
retourner F;
L'exécution d'un tel algorithme sur l'arbre binaire de l'exemple 5.2 retourne la file (n1,n2,n4,n5,n3,n6).
5-1-2. Écriture itérative d'un parcours en profondeur▲
L'exécution d'un algorithme récursif pouvant être coûteuse en espace mémoire, il est souvent préférable de fournir une version itérative.
Une version itérative équivalente à l'algorithme parcoursArbre est celle décrite sur la Figure 5.4.
5-2. Parcours en largeur▲
Un second parcours d'un arbre consiste à traiter la racine, puis ses fils, ses petits-fils et ainsi de suite. Ainsi, lors de ce parcours, sont traités les nœuds à distance 0 de la racine (la racine), puis ceux à distance 1, puis ceux à distance 2 et ainsi de suite.
La définition d'un tel parcours nécessite une file et peut être celle décrite par la Figure 5.5.
Exemple 13 Sur l'exemple de l'arbre binaire de la Figure 5.2, l'exécution de l'algorithme entraîne l'exécution des instructions suivantes :
2.
3.
4.
5.
6.
traiter1(n1); traiter2(n1);
traiter1(n2); traiter2(n2);
traiter1(n3); traiter2(n3);
traiter1(n4); traiter2(n4);
traiter1(n5); traiter2(n5);
traiter1(n6); traiter2(n6);
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
procédure parcoursArbreProfondeurItératif(T:arbre)
si non(estVide(T)) alors
P ← empiler((racine(T),0),pileVide());
tantque non(estVide(P)) faire
(n,i) ← tete(P);
P ← depiler(P);
si estSentinelle(n) alors
traiter4(n);
sinon si i=0 alors
P ← empiler((n,3),P);
P ← empiler((filsDroit(n),0),P);
P ← empiler((n,2),P);
P ← empiler((filsGauche(n),0),P);
P ← empiler((n,1),P);
sinon si i=1 alors
traiter1(n);
sinon si i=2 alors
traiter2(n);
sinon
traiter3(n);
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
procédure parcoursLargeur(T:arbre)
si non(estVide(T))
F ← enfiler(racine(n),fileVide());
tantque non(estVide(F)) faire
n ← premier(F);
F ← defiler(F);
traiter1(n);
si non(estSentinelle(n)) alors
F ← enfiler(filsGauche(n),F);
F ← enfiler(filsDroit(n),F);
traiter2(n);
6. Chapitre 6 - Arbres binaires de recherche▲
Les arbres binaires de recherche permettent d'implémenter de façon très efficace les multiensembles en permettant d'accéder à un élément en un temps qui dépend non de la cardinalité de l'ensemble, mais de la hauteur de l'arbre qui le représente.
6-1. Définitions▲
Définition 5 Un arbre binaire de recherche (abrégé en A.B.R.) est un arbre binaire dans lequel la clé de tout nœud n
- Est strictement supérieure à la clé de tout nœud du sous-arbre gauche de n ;
- Est strictement inférieure à la clé de tout nœud du sous-arbre droit de n.
Exemple 14 Un exemple d'arbre binaire de recherche est celui décrit par la Figure 6.1.
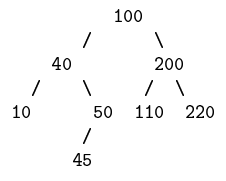
Aussi, nous supposerons que le type nœud est enrichi d'une fonction qui lui fournit la clé :
|
clé |
: nœud |
→ entier |
6-2. Le problème Recherche▲
Résoudre le problème de recherche :
|
Recherche |
est résolu aisément à l'aide de la fonction rechercheArbre utilisant une fonction récursive recherche définie par la Figure 6.2.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
fonction rechercheArbre(T:arbre,k:entier):booléen x nœud
retourner recherche(racine(T),k);
fonction recherche(n:nœud,k:entier):booléen x nœud
si estSentinelle(n)
retourner (faux,_);
sinon si k=clé(n)
retourner (vrai,n);
sinon si k < clé(n)
retourner recherche(filsGauche(n),k);
sinon
retourner recherche(filsDroit(n),k);
Exercice 8 Prouver que recherche est correct, c'est-à-dire résout le problème Recherche.
Exercice 9 Prouver que la complexité en temps dans le pire des cas de recherche est kitxmlcodeinlinelatexdvpO(h)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp est la hauteur de l'arbre T.
Exercice 10 Écrire de façon itérative l'algorithme recherche.
6-3. Insertion d'un nouveau nœud▲
Pour insérer un nouveau nœud x dans un arbre T, on parcourt l'arbre de façon similaire à l'algorithme recherche jusqu'à trouver un nœud y sans fils gauche et de clé supérieure (resp. ou sans fils droit et de clé inférieure). À cet instant, on place x fils gauche (resp. droit) de y.
Afin de simplifier l'écriture, on supposera que le nœud n a pour père, pour fils gauche et pour fils droit trois nœuds sentinelles. L'algorithme insérer est décrit sur la Figure 6.3.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
fonction insérer(T:arbre, n:nœud) arbre
si estVide(T)
retourner changerRacine(T,n);
sinon
x ← racine(T);
faire
y ← x;
si clé(n) < clé(x)
x ← filsGauche(x);
àGauche ← vrai();
sinon
x ← filsDroit(x);
àGauche ← faux();
jusqu'à estSentinelle(x)
si àGauche
y ← changerFilsGauche(y,n);
sinon
y ← changerFilsDroit(y,n);
retourner (T);
Exercice 11 Prouver la correction de insérer.
Exercice 12 Prouver que la complexité en temps dans le pire des cas de insérer est kitxmlcodeinlinelatexdvpO(h)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp est la hauteur de l'arbre T.
6-4. Le problème du successeur▲
Définition 6 Dans un A.B.R., un nœud o est successeur d'un nœud n si aucun nœud de l'arbre ne possède une clé strictement comprise entre clé(n) et clé(o).
Exemple 15 Dans le cas de l'arbre de la figure 6.1, le nœud de clé 50 a pour père le nœud de clé 100.
Fait 4 Un nœud z a pour successeur y si et seulement si :
- x a un fils droit et y est le nœud de clé minimale dans le sous-arbre droit de x ;
- x n'a pas de fils droit et y est le plus proche ancêtre de x dont le fils gauche est ancêtre de x.
preuve :
La preuve est laissée au lecteur.
La fonction suivante requiert une routine auxiliaire qui calcule le nœud de clé minimale parmi les descendants d'un nœud n, lui y compris. Cette routine est définie par la Figure 6.4.
2.
3.
4.
5.
6.
fonction minimumDescendants(n:nœud): nœud
tantque ?FilsGauche(n) faire
n ← filsGauche(n);
retourner n;
Conséquence directe du Fait 4, la définition et la correction de l'algorithme qui calcule le successeur d'un nœud (Figure 6.5).
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
fonction successeur(T:arbre; n : nœud) : nœud
si ?FilsDroit(n)
retourner minimumDescendants(filsDroit(n));
sinon
p ← père(n);
tantque non(estSentinelle(p)) et n ≠ filsGauche(p)
n ← p;
p ← père(p);
retourner(p);
Exercice 13 Prouver que la complexité dans le pire des cas de successeur est en espace de kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp et en temps de kitxmlcodeinlinelatexdvpO(h)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp est la hauteur de l'arbre T.
6-5. Suppression d'un nœud dans un arbre binaire▲
Le problème qu'on souhaite résoudre ici est la suppression d'un nœud n dans un arbre binaire de recherche de façon naturellement à conserver un arbre binaire de recherche. Deux premiers cas simples se présentent alors :
- n n'a aucun fils.
La situation est évidente : on supprime le nœud n ; - n possède un seul fils.
La situation est tout aussi évidente : on déclare l'unique fils de n fils du père de n. On réalise l'opération dite de détachement.
Écrivons dès à présent cette fonction détacher (Figure 6.7) qui prend pour argument un arbre binaire T et un nœud x (qui n'est pas une sentinelle) possédant au plus un fils et qui supprime dans l'arbre binaire le nœud x en plaçant son éventuel unique fils comme fils gauche (resp. droit) du père de x si x est fils gauche (resp. droit) de son père. Observons que cette fonction dans le cas où x n'a aucun fils, supprime simplement le nœud x.
Exemple 16 Un exemple de détachement est celui décrit par la Figure 6.6. Le nœud 50 est supprimé, son ancien père (le nœud 40) prend pour nouveau fils droit l'ancien fils gauche du nœud 50 à savoir le nœud 45.
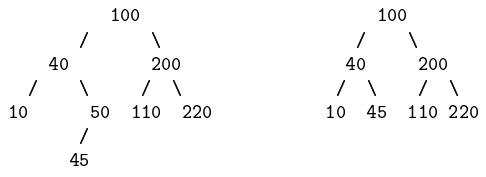
En ce qui concerne le problème de suppression, un troisième cas se distingue :
- n possède deux fils.
On considère son nœud successeur y. Celui-ci est nécessairement un descendant de n (n possède un fils droit) et donc ne peut pas posséder de fils gauche. Il suffit alors que le père de y prenne pour nouveau fils, le fils droit de y (opération de détachement de y) et que y prenne la place de n pour obtenir un arbre binaire de recherche.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
fonction détacher(T : arbre; x : nœud) : arbre
si ?FilsDroit(x)
f ← filsDroit(x);
sinon
f ← filsGauche(x);
si estRacine(T,x) alors
T ← changerRacine(T,f);
sinon
p ← père(x);
si filsGauche(p)=x
p ← changerFilsGauche(p,f);
sinon % on a filsDroit(p)=x
p ← changerFilsDroit(p,f);
retourner T;
Exemple 17 Un exemple de suppression d'un nœud (le nœud 100) ayant deux fils est celui décrit par la Figure 6.8. Sur cet exemple, nous voyons que le nœud 100 est remplacé par son successeur ( le nœud 110) et que celui-ci est détaché (car n'ayant pas de fils gauche), son ancien père (le nœud 200 prend pour nouveau fils gauche l'ancien fils droit de 110 à savoir le nœud 130).
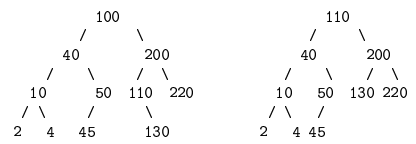
L'algorithme de suppression est décrit dans la Figure 6.9.
2.
3.
4.
5.
6.
7.
fonction supprimer(T:arbre; x : nœud): arbre
si non(?FilsGauche(x)) OU non(?FilsDroit(x))
retourner détacher(T,x);
sinon
s ← successeur(T,x);
x ← changerContenu(x,contenu(s));
retourner détacher(T,s);
Remarque
Dans l'algorithme détacher, nous avons autorisé la comparaison de deux nœuds en évaluant l'expression filsGauche(p) = x. Or dans le type abstrait nœud, cette possibilité n'était pas offerte. Deux solutions s'offrent à nous :
-
On enrichit le type abstrait d'une opération permettant de tester l'égalité entre deux nœuds :
égalité
: nœud x nœud
→ booléen
- On ramène l'égalité de deux nœuds en comparant leur clé (sachant que les clés caractérisent les nœuds). En clair, on remplace expression filsGauche(p) = x par clé(filsGauche(p)) = clé(x).
6-6. Conclusion▲
Nous avons vu que la complexité en temps des fonctions insérer, supprimer et recherche est au plus égale à la hauteur de l'arbre.
Cette majoration est une bonne nouvelle, car non seulement il existe des arbres de grande taille n et de hauteur kitxmlcodeinlinelatexdvplog_2(n)finkitxmlcodeinlinelatexdvp (par exemple des arbres binaires parfaits), mais de plus tous le sont ou presque : on démontre sans trop de difficulté qu'un arbre binaire de recherche construit aléatoirement de taille n est de taille kitxmlcodeinlinelatexdvp3 \cdot log_2(n)finkitxmlcodeinlinelatexdvp.
Ainsi, « sans malchance », la complexité en temps est kitxmlcodeinlinelatexdvpO(log_2(n))finkitxmlcodeinlinelatexdvp.
Ce propos malheureusement n'empêche pas des situations d'infortune. En effet, si l'arbre de recherche est dégénéré c'est-à-dire de hauteur proche de sa taille (par exemple des arbres dans lesquels chaque nœud a très souvent au plus un unique fils), la complexité est kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp.
Il existe de nombreuses techniques qui permettent de maintenir un arbre équilibré c'est-à-dire vérifiant hauteur(T) = log{taille(T)). Les familles d'arbres de recherches équilibrés sont d'arité :
- 2. Les arbres rouges et noirs sont un exemple ;
- 3. Chaque nœud possède au plus trois fils. Les 2,3-arbres sont un exemple.
7. Chapitre 7 - Les arbres rouges et noirs▲
Nous présentons dans ce chapitre un ensemble de techniques permettant d'implémenter le type ensemble :
|
estVide |
: ensemble |
→ booléen |
|
ensembleVide |
: |
→ ensemble |
|
choisir |
: élément |
→ élément |
|
appartient |
: élément x ensemble |
→ booléen |
|
ajouter |
: élément x ensemble |
→ ensemble |
|
enlever |
: élément x ensemble |
→ ensemble |
selon une complexité en espace kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp et, en notant n la cardinalité de l'ensemble manipulé, selon une complexité en temps dans le pire des cas égale à :
|
estVide |
: kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp |
|
ensembleVide |
: kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp |
|
choisir |
: kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp |
|
appartient |
: kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp |
|
ajouter |
: kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp |
|
enlever |
: kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp |
Nous avons vu dans le dernier chapitre que la représentation d'un ensemble E à l'aide d'un arbre binaire de recherche T garantissait une complexité en temps égale à kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp pour les trois premières fonctions et égale à kitxmlcodeinlinelatexdvpO(hauteur(T))finkitxmlcodeinlinelatexdvp pour les trois dernières.
Observant que tout arbre binaire a une hauteur au moins égale à kitxmlcodeinlinelatexdvplog(n)finkitxmlcodeinlinelatexdvp (plus exactement à kitxmlcodeinlinelatexdvp\left \lfloor log(n) \right \rfloorfinkitxmlcodeinlinelatexdvp), pour obtenir une complexité en kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp, il suffit de manipuler des arbres binaires de recherche T vérifiant
kitxmlcodelatexdvphauteur (T) = O(log(taille(T)))finkitxmlcodelatexdvpPlusieurs familles de tels arbres existent, celle que nous présentons ici est : les arbres rouges et noirs.
7-1. Définition▲
Un arbre rouge et noir est un arbre binaire de recherche tel que :
- Chaque nœud est colorié ou en rouge ou en noir ;
- Chaque sentinelle est coloriée en noir ;
- Si un nœud est rouge, ses deux fils sont noirs ;
- Chaque chemin de la racine à une feuille contient le même nombre de nœuds noirs.
Fait 5 Tout arbre rouge et noir T vérifie : kitxmlcodeinlinelatexdvphauteur (T) = O(log(taille(T)))finkitxmlcodeinlinelatexdvp
En fait nous avons : kitxmlcodeinlinelatexdvp\left \lfloor log(taille(T)) \right \rfloor \le hauteur(T) \le 2 \cdot log(taille(T)))finkitxmlcodeinlinelatexdvp
preuve :
Pour tout arbre rouge et noir T, notons noir(T) l'arbre (non binaire) obtenu à partir de T en coloriant en noir sa racine (voir Exercice 14) et en rattachant chaque fils d'un nœud rouge à son grand-père nécessairement noir. Il vient :
Tout fils d'un sommet rouge étant noir, il vient :
kitxmlcodelatexdvphauteur(T) \le 2 \cdot (hauteur(noir(T)))finkitxmlcodelatexdvpClairement, noir(T) est un arbre dont tout chemin de la racine à l'une des feuilles est de longueur constante égale à hauteur(noir(T)) et dont chaque nœud possède au moins deux fils, il en découle :
kitxmlcodelatexdvphauteur(noir(T)) \le log(taille(noir(T)))finkitxmlcodelatexdvpCe qui suffit à conclure.
Exercice 14 Démontrer qu'en coloriant en noir la racine d'un arbre rouge et noir, on conserve un arbre rouge et noir.
7-2. Une opération locale : la rotation▲
Voici deux opérations qui transforment tout arbre binaire de recherche en un arbre binaire de recherche :
Définition 7 Soit T un arbre rouge et noir. Soit y un nœud dont le fils gauche x n'est pas une sentinelle. Nous notons rotationDroite(T,y) l'arbre obtenu à partir de T en prenant :
- Pour nouveau père de x l'ancien père de y ;
- Pour nouveau fils gauche de y l'ancien fils droit de x ;
- Pour nouveau fils droit de x le nœud y.
Soit x un nœud de T dont le fils droit y n'est pas une sentinelle. Nous notons rotationGauche(T,x) l'arbre obtenu à partir de T en prenant :
- Pour nouveau père de y l'ancien père de x ;
- Pour nouveau fils droit de x l'ancien fils gauche de y ;
- Pour nouveau fils gauche de y le nœud x.
Exercice 15 Écrire un algorithme de complexité en temps kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp réalisant la rotation gauche.
Exercice 16 En reprenant les notations de la définition précédente, démontrer que l'arbre T est égal aux deux arbres :
rotationGauche(rotationDroite(T,y) ,x)
rotationDroite(rotationGauche(T,x),y)Exercice 17 Démontrer que tout arbre binaire de recherche peut être transformé en une « chaîne droite » en au plus n - 1 rotations. En déduire que tout arbre binaire de recherche peut être transformé en tout autre arbre binaire de recherche possédant les mêmes nœuds en au plus 2·(n - 1) rotations.
7-3. Insérer un nœud▲
Le problème d'insertion :
|
problème RN-insérer |
admet comme solution l'algorithme de la Figure 7.1. Afin de simplifier l'écriture, nous utiliserons une procédure colorationRouge qui permet de colorier en rouge tout sommet (ainsi la notation colorationRouge(n) remplace n ← colorationRouge(n).
De plus, nous utilisons de nouvelles primitives frère, estFilsGauche à signification évidente dont l'écriture est laissée en exercice.
Exercice 18 Écrire les algorithmes frère, estFilsGauche, oncle.
7-3-1. Correction sommaire▲
Pour prouver la correction de cet algorithme, il suffit de démontrer l'invariance de la propriété suivante : l'arbre T est un arbre rouge et noir exception faite que le nœud x et son père peuvent être rouges.
En conséquence, à la sortie de boucle tantque, il est assuré que ou x est racine ou que son père est noir. Ainsi, l'arbre T retourné est rouge et noir.
7-3-2. Complexité▲
Il est assez immédiat d'observer qu'à chaque passage de boucle, la distance de x à la racine diminue strictement. La hauteur de l'arbre étant initialement kitxmlcodeinlinelatexdvplog(n)finkitxmlcodeinlinelatexdvp, la complexité en temps est kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp.
7-4. Suppression▲
Le problème de suppression d'un nœud :
|
problème RN-supprimer |
admet comme solution l'algorithme défini par les Figures 7.2 et 7.3.
7-4-1. Correction très sommaire▲
Conséquence du fait que la modification de l'arbre n'est réalisée qu'au travers de rotations gauches et droites, l'arbre conserve l'ensemble de nœuds initial et demeure un arbre binaire de recherche tout au long de l'algorithme.
Reste à démontrer que l'arbre retourné est un arbre rouge et noir. Cette preuve est présentée au tableau noir de l'amphithéâtre par utilisation de craies rouges.
7-4-2. Complexité▲
Infortunément à chaque passage de boucle, le sommet x ne se rapproche pas de la racine, ainsi dans le cas où son frère est rouge, une conséquence de la rotation est que, dans le nouveau nœud z peut rester à une même distance de la racine que l'ancien nœud z. Cependant, dans ce cas, on est assuré que le nouveau nœud x a un frère noir, ce qui permet par le prochain passage de boucle de se rapprocher strictement de la racine.
Ainsi, après deux passages de boucle consécutifs, la distance de x à la racine décroît strictement. Toutes les instructions de l'algorithme correction étant de complexité en temps kitxmlcodeinlinelatexdvpO(1)finkitxmlcodeinlinelatexdvp, on déduit que correction est de complexité en temps kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp.
On étend naturellement ce résultat à détacher et RN-supprimer.
Exercice 19 Est-ce que pour tout nœud x et pour tout arbre rouge et noir T, l'arbre T est égal à RN-supprimer(RN-insérer(T,x),x) ?
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
fonction RN-insérer(T : RN-arbre; x : nœud) : RN-arbre
colorationRouge(x);
colorationNoir(racine(T));
T ← insérer(T,x);
tantque x ≠ racine(T) et couleur(père(x)) = rouge faire
si estFilsGauche(père(x)) alors
si couleur(oncle(x)) = rouge alors
colorationNoir(père(x));
colorationNoir(oncle(x));
colorationRouge(père(père(x)));
x ← père(père(x));
sinon
si estFilsDroit(x) alors
T ← rotationGauche(T,père(x));
x ← filsGauche(x);
colorationNoir(père(x));
colorationRouge(père(père(x)));
T ← rotationDroite(T,père(père(x)));
sinon % même instruction en échangeant gauche et droite
retourner(T);
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
fonction RN-supprimer(T: RN-arbre; y : nœud) : RN-arbre
si ?FilsGauche(y) ET ?FilsDroit(y) alors
y ← changerContenu(y,successeur(T,y));
y ← successeur(T,y);
si ?FilsGauche(y) alors
x ← filsGauche(y);
sinon
x ← filsDroit(y);
T ← détacher(T,y);
si couleur(y) = rouge alors
retourner T;
sinon
retourner correction(T,x);
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
fonction correction(T: RN-arbre; x : nœud) : RN-arbre
tantque x ≠ racine(T) ET couleur(x) = noir faire
si estFilsGauche(x) alors
w ← frère(x);
si couleur(w)=rouge alors
colorationNoir(w);
colorationRouge(père(x));
T ← rotationGauche(T,père(x));
w ← frère(x);
% on a couleur(w)=noir
si couleur(filsGauche(w))=noir ET couleur(filsDroit(w))=noir alors
colorationRouge(w);
colorationNoir(père(x));
x ← père(x);
sinon
si couleur(filsGauche(w)) = rouge alors
colorationNoir(filsGauche(w));
colorationRouge(w);
T ← rotationDroite(T,w);
w ← filsDroit(père(x));
% on a couleur(filsGauche(w))=noir
% et couleur(filsDroit(w))=rouge
si couleur(père(x)) = noir alors
colorationNoir(filsDroit(w));
T ← rotationGauche(T,père(x));
x ← racine(T);
retourner T;
8. Chapitre 8 - Le type partition▲
Un objet commun en mathématique est la notion de partition d'un ensemble E. Nous montrons dans ce chapitre commet implémenter efficacement des partitions à l'aide d'arbres et obtenir des instructions de complexité en temps constante !
8-1. Préalables mathématiques▲
Une partition d'un ensemble E est un ensemble de parties de E non vides deux à deux disjointes (d'intersection vide) dont l'union forme E.
Rappelons que la notion de partition d'un ensemble est identique à la notion de relation d'équivalence, une relation d'équivalence est une relation réflexive, symétrique et transitive :
-
Toute partition kitxmlcodeinlinelatexdvpPfinkitxmlcodeinlinelatexdvp d'un ensemble kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp admet pour relation d'équivalence la relation kitxmlcodeinlinelatexdvp\simfinkitxmlcodeinlinelatexdvp qui relie deux objets appartenant à une même partie de E :
kitxmlcodeinlinelatexdvpa \sim b: \Leftrightarrow \exists A \in P\{a,b\} \subseteq Afinkitxmlcodeinlinelatexdvp ;
- Inversement, toute relation d'équivalence sur un ensemble kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp induit comme partition celle composée des classes d'équivalence :
La partition discrète d'un ensemble kitxmlcodeinlinelatexdvpFfinkitxmlcodeinlinelatexdvp est la partition composée des singletons kitxmlcodeinlinelatexdvp\{\{a\}\ | a \in E\}finkitxmlcodeinlinelatexdvp.
Nous appellerons union l'opération qui associe à une partition kitxmlcodeinlinelatexdvpPfinkitxmlcodeinlinelatexdvp d'un ensemble kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp et à deux éléments non équivalents kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp la partition obtenue à partir de kitxmlcodeinlinelatexdvpPfinkitxmlcodeinlinelatexdvp en réalisant l'union des classes de kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp.
8-2. Un type abstrait partition▲
Suite aux définitions précédentes, nous définissons le type abstrait suivant :
|
Type Partition |
||
|
Utilise : booléen, ensemble |
||
|
Opérations |
||
|
partitionDiscrete |
: ensemble |
→ partition |
|
equivalent |
: partition x élément x élément |
→ booléen |
|
union |
: partition x élément x élément |
→ partition |
8-3. Quelques premières implémentations▲
8-3-1. À l'aide de séquences et de listes chaînées▲
Une première implémentation consiste à définir chacune des classes à l'aide d'une séquence.
Exemple 18 La partition {{1,4,6},{2,5},{3}} se représente par exemple à l'aide de l'ensemble {(1,6, 4), (2, 5), (3)}.
Décider si deux éléments a et b sont équivalents nécessite alors de tester l'appartenance de a à la séquence contenant b.
Si la séquence est représentée à l'aide d'une liste chaînée, ce test est de complexité en temps linéaire.
8-3-2. À l'aide d'étoiles (arbres de hauteur 1)▲
Pour réaliser le test d'équivalence en temps constant, il est nécessaire d'associer pour chaque élément en temps constant un objet qui caractérise la classe à laquelle il appartient.
Une solution est d'associer à chaque élément un élément singulier de sa classe d'équivalence, que nous appellerons son représentant. L'objet ainsi défini peut se définir de façon équivalente comme ;
- Un objet mathématique : une fonction kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp de kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp dans kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp vérifiant kitxmlcodeinlinelatexdvpf \circ f = ffinkitxmlcodeinlinelatexdvp ;
- Un objet informatique : un tableau à indices dans kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp à valeurs dans kitxmlcodeinlinelatexdvpEfinkitxmlcodeinlinelatexdvp ;
- Un objet graphique : une étoile.
Exemple 19 Ainsi, la partition {{1, 4,6}, {2,5}, {3}} se représente par exemple à l'aide du tableau T :
|
1 |
2 |
3 |
4 |
5 |
6 |
|
4 |
2 |
3 |
4 |
5 |
4 |
Ainsi tester l'équivalence de deux éléments a et b se fait en temps constant : il suffit de tester l'égalité T[a]=T[b].
Malheureusement, si l'on souhaite réaliser l'union de deux éléments, il est nécessaire pour l'une des deux classes dont on souhaite faire l'union de modifier l'objet caractéristique de cette classe. Cette modification doit concerner chacun des éléments de cette classe. Sa complexité en temps est proportionnelle à la cardinalité de cette classe et est donc linéaire.
8-4. Implémentation à l'aide d'arbres▲
Une idée consiste à considérer un objet plus complexe que l'étoile à savoir un arbre : ainsi toute classe est représentée à l'aide d'un arbre dont la racine est le représentant.
Exemple 20 Ainsi, la partition {{1,4,6,8,9,10},{2,5,7},{3}} se représente par exemple à l'aide des trois arbres :
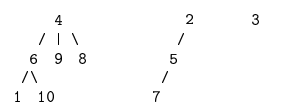
Calculer le représentant d'un élément nécessite alors de calculer la racine de l'arbre auquel il appartient.
Décider si deux éléments sont équivalents revient à calculer puis à comparer leur représentant.
Réaliser l'union de deux éléments revient à calculer leur représentant puis à placer l'un des deux représentants fils de l'autre représentant.
Ainsi, les opérations sur ces arbres ne consistent qu'à « remonter » dans l'arbre afin de calculer la racine ascendante d'un élément courant. Une représentation optimale d'un arbre est de le représenter à l'aide d'un simple tableau indiquant pour chaque élément son père (pour des raisons de simplicité, on considèrera le père de la racine égale à la racine elle-même).
Exemple 21 Ainsi, l'ensemble des trois arbres représentant la partition {{1, 4, 6, 8,9, 10}, {2, 5,7}, {3}}
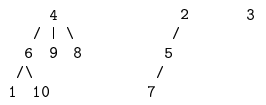
est représenté à l'aide du tableau :
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
6 |
2 |
3 |
4 |
2 |
4 |
5 |
4 |
4 |
6 |
8-4-1. Une première implémentation▲
Pour des raisons de simplification, nous supposerons que l'univers E forme un intervalle d'entiers de la forme kitxmlcodeinlinelatexdvp[1,i]finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvpi \ge 0finkitxmlcodeinlinelatexdvp. Ainsi, la signature de partitionDiscrete devient :
|
partitionDiscrete |
: entier |
→ partition |
En implémentant une partition comme une structure contenant pour seul champ un champ de nom père de type tableau, nous obtenons :
2.
3.
4.
5.
6.
7.
8.
9.
fonction partitionDiscrete(n : entier) : partition
tab ← tableau(n)(1);
pour i de 1 à n faire
tab[i] ← i
p ← structure(pere)(tab);
retourner p;
Conformément à la section précédente, nous enrichissons le type abstrait de l'opération :
|
représentant |
: partition x élément |
→ élément |
qui a pour implémentation :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
fonction représentant(p:partition; a : élément) :élément
si p.pere[a] ≠ a alors
retourner représentant(p, p.pere[a])
sinon
retourner p.pere[a];
fonction équivalent(p:partition; a : élément; b : élément): booléen
retourner représentant(p,a) = représentant(p,b)
fonction union(p:partition; a : élément; b : élément): partition
a ← représentant(p, a);
b ← représentant(p, b);
p.pere[a] ← b;
retourner p;
La complexité en temps de union ou équivalent dépend de la complexité de représentant qui est exactement la profondeur dans l'arbre de l'élément a, à savoir la distance de celui-ci à la racine qui peut être égale à la taille de l'arbre.
Exercice 20 Dessiner la partition retournée par l'algorithme suivant. Démontrer que le programme suivant a une complexité en temps égale à kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp.
2.
3.
4.
5.
6.
7.
fonction test(n:entier) : partition
p ← partitionDiscrete(n);
pour i de 2 à n faire
p ← union(p,1,i);
retourner p;
Exercice 21 Dessiner la partition retournée par l'algorithme suivant. Démontrer que le programme suivant a une complexité en temps égale à kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp.
2.
3.
4.
5.
6.
7.
fonction test(n:entier) : partition
p ← partitionDiscrete(n);
pour i de 2 à n faire
p ← union(p,i-1,i);
retourner p;
8-4-2. Une seconde implémentation▲
Une première idée : transformation dynamique de l'arbre
Afin de diminuer ces complexités en temps, une première idée consiste chaque fois que l'on calcule le représentant r d'un élément a de profiter de ce calcul pour modifier l'arbre de façon à ce que le prochain calcul soit plus rapide. Dans notre cas, il suffit d'écraser l'arbre en faisant de a et de tous ses ascendants des fils de r.
Exemple 22 Ainsi, le calcul du représentant de l'élément 11 dans l'arbre de gauche modifiera l'arbre à gauche de la Figure 8.1 en l'arbre dessiné à droite :
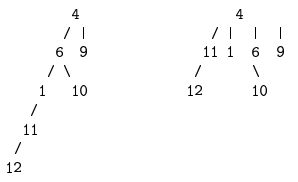
L'algorithme permettant de calculer le représentant d'un élément est défini sur la Figure 8.2. Il nécessite une fonction auxiliaire permettant de calculer l'ensemble des nœuds ascendants d'un nœud donné (algorithme de la Figure 8.3).
2.
3.
4.
5.
6.
7.
8.
9.
10.
fonction représentant2(p:partition; a : élément) :élément x partition
ascendants ← calculAscendants(p, a);
(r,ascendants) ← extraire(ascendants);
tantque est(nonVide(ascendants)) faire
(b,ascendants) + extraire(ascendants);
p.pere[b] + r;
retourner (r,p);
Une seconde idée : minimisation des hauteurs.
Afin d'obtenir des arbres de hauteur minimale, on enrichit la partition d'une information sur chacun des éléments appelée son poids, mesurant en fait l'importance du nœud racine. Ce poids n'est modifié que lorsqu'une racine admet pour nouveau fils un élément de même poids.
Les algorithmes deviennent :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
fonction partitionDiscrete2(n : entier) : partition
tab ← tableau(n)(1);
poids ← tableau(n)(0);
pour i de 1 à n faire
tab[i] ← i
p ← structure(pere,poids)(tab,poids);
retourner p;
fonction calculAscendants(p:partition; a : élément) : pile
ascendants ← empiler(a,pileVide());
tantque a ≠ p.pere[a] faire
a ← p.pere[a];
ascendants ← empiler(a,ascendants);
retourner ascendants;
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
fonction union2(p:partition; a : élément; b : élément): partition
(a,p) ← representant2(p , a);
(b,p) ← representant2(p , b);
si p.poids[a] > p.poids[b] alors
p.pere[b] ← a;
sinon
p.pere[al ← b;
si p.poids[al=p.poids [b] alors
p.poids[b] ← p.poids[b]+1;
retourner p;
8-4-3. Calcul des complexités▲
Complexité logarithmique
Il est aisé d'observer qu'un élément a fils d'un élément b a un poids strictement inférieur. Ainsi, la hauteur d'un arbre n'excède pas le poids de sa racine.
On peut démontrer que tout arbre dont la racine est de poids p possède au moins 2p éléments.
Conséquence de ces deux observations, la complexité en temps dans le pire des cas de union2, représentant2 ainsi que equiv est kitxmlcodeinlinelatexdvpO(log(n))finkitxmlcodeinlinelatexdvp.
Exercice 22 Démontrer que tout arbre dont la racine est de poids p possède au moins 2p éléments.
Complexité amortie (quasi) constante
En réalité, nous avons un résultat de complexité bien plus intéressant. Pour cela nous ne considérons pas la complexité dans le pire des cas de chaque exécution d'une des fonctions, mais nous considérons un programme globalement. Considérons un programme lors duquel est créée une partition de n éléments et lors duquel sont exécutées m instructions union2, représentant2 ou equiv.
Il est alors possible de prouver (une preuve est disponible dans le chapitre 22 du Cormen) que le coût total de ces m instructions est kitxmlcodeinlinelatexdvpO(m \cdot \log^*(n))finkitxmlcodeinlinelatexdvp, ce qui ramène le coût (amorti) de chaque instruction à un coût (quasi) constant (voir la définition de kitxmlcodeinlinelatexdvplog^*(n)finkitxmlcodeinlinelatexdvp ci-dessous).
Présentation succincte de kitxmlcodeinlinelatexdvplog^*(n)finkitxmlcodeinlinelatexdvp
Une définition précise de kitxmlcodeinlinelatexdvplog^*(n)finkitxmlcodeinlinelatexdvp est disponible dans le Cormen. Disons simplement que kitxmlcodeinlinelatexdvplog^*(n)finkitxmlcodeinlinelatexdvp est une fonction kitxmlcodeinlinelatexdvp\mathbb{N}\rightarrow \mathbb{N}finkitxmlcodeinlinelatexdvp croissante qui associe à tout entier de la forme kitxmlcodeinlinelatexdvp2^{2^{2^{.^{.^{.^{2}}}}}}finkitxmlcodeinlinelatexdvp son nombre de niveaux. Nous avons : kitxmlcodeinlinelatexdvplog^*(2) = 1finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvplog^*(2^2) = 2finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvplog^*(2^4) = 3finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvplog^*(2^{16}) = 4finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvplog^*(2^{65536}) = 5finkitxmlcodeinlinelatexdvp, etc.
En conséquence de quoi, un entier kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp pour lequel kitxmlcodeinlinelatexdvplog^*(x) \ge 5finkitxmlcodeinlinelatexdvp est au moins égal à kitxmlcodeinlinelatexdvp2^{65536}finkitxmlcodeinlinelatexdvp et est donc bien supérieur au nombre d'atomes présents dans l'univers observable (évalué à kitxmlcodeinlinelatexdvp10^{80} \simeq 2^{265}finkitxmlcodeinlinelatexdvp).
Ainsi, d'un point de vue pratique, kitxmlcodeinlinelatexdvplog^*(n)finkitxmlcodeinlinelatexdvp doit être considéré comme constant : nous ne manipulerons jamais une partition de cardinalité supérieure à kitxmlcodeinlinelatexdvp2^{65536}finkitxmlcodeinlinelatexdvp.
8-5. Utilisation de partition▲
Le premier ascendant commun de deux nœuds dans un arbre est ascendant commun de plus grande profondeur. On considère ici qu'un nœud est ascendant de lui-même.
Si nous souhaitons calculer le premier ascendant commun à deux nœuds, il est nécessaire de remonter (éventuellement totalement) les deux chemins allant de ces deux nœuds en direction de la racine. La complexité est alors au moins la différence de la profondeur de cet ascendant avec celle du nœud le plus profond. Dans le pire des cas, cette complexité peut être la hauteur de l'arbre et donc la taille de l'arbre.
Le problème auquel nous nous intéressons est de calculer dans un arbre pour un ensemble de couples C le premier ascendant commun de chacun des couples. Si nous utilisons une méthode naïve qui consisterait, pour chacun des couples à calculer le premier ascendant commun, nous obtiendrons un algorithme en kitxmlcodeinlinelatexdvpO(n \times m)finkitxmlcodeinlinelatexdvp.
L'algorithme présenté ici est de complexité en temps optimale, car linéaire (égal à kitxmlcodeinlinelatexdvpO(n + m)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp est le nombre de sommets de l'arbre et kitxmlcodeinlinelatexdvpmfinkitxmlcodeinlinelatexdvp le nombre de couples de C).
Exemple 23 Ainsi, si T est l'arbre dessiné ci-dessous :
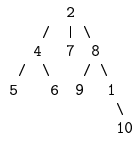
et si C est l'ensemble ((4, 7), (5, 1), (10, 9), (8, 10)), nous souhaitons calculer l'ensemble des triplets :
- ((4, 7, 2), (5, 1, 2), (4, 9, 2), (10, 9, 8), (8, 10, 8)).
L'algorithme consiste en un parcours en profondeur de l'arbre selon un traitement postfixe. L'ensemble des nœuds traités sont coloriés en noir. Traiter un nœud u consiste à traiter ses fils, puis à calculer l'ascendant de u avec chacun des nœuds noirs souhaités. Afin de simplifier les notations, les variables couleur, ascendant, partition, solution sont considérées comme globales. L'algorithme est le suivant et est défini récursivement à l'aide de la fonction parcours (Figure 8.4).
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
fonction premierAscendant(T:arbre; C : ensemble de couples) : ensemble
n ← taille(T);
partition ← partitionDiscrete(n);
ascendant ← tableau(n)(0);
pour i de 1 à n faire
couleur ← tableau(n)(blanc);
solution ← ensembleVide();
premierAscendantRec(racine(T));
retourner solution;
La définition de premierAscendantRec colorie des sommets en gris ; cette coloration n'est pas utilisée à l'exécution de l'algorithme (le seul test réalisé est de tester si un sommet est noir). Cet ajout permet une meilleure compréhension de l'algorithme : lors de l'étude la correction de l'algorithme, nous verrons que ces sommets gris forment un chemin de la racine au sommet couramment parcouru.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
procédure premierAscendantRec(u : nœud)
couleur[u] ← gris;
pour chaque fils v de u dans T faire
premierAscendantRec(v);
partition ← union(partition,u,v);
ascendant[representant[u]] ← u
pour chaque nœud w tel que {u,w} ∈ C et couleur[w]=noir faire
solution ← ajouter(solution, (u,w,ascendant[representant(w)]);
couleur[u] ← noir;
Correction
La correction de cet algorithme est la conséquence de l'invariance des propriétés suivantes :
- Si un nœud est gris, son père est gris ;
- Si un nœud est noir, son père est ou gris ou noir ;
- Un nœud est noir si tous ses fils le sont ;
- Un nœud admet au plus un fils gris ;
- Les nœuds gris forment un chemin dont l'une des extrémités est la racine et dont la seconde est le nœud u parcouru ;
- Pour tout nœud noir w, le nœud ascendant[representant(w)] est un ascendant de w qui est gris, mais dont le fils qui est ascendant de w est noir.
Conséquence de ces propriétés, tout premier ascendant commun d'un nœud noir w et d'un nœud gris u est un nœud gris. Puisque le nœud u considéré dans l'algorithme est le prochain nœud colorié en noir, tout sommet gris est ascendant de u. Ainsi, le nœud gris ascendant[representant(w)] est un ascendant commun à u et w et est le premier puisque son unique fils qui est ascendant de w est noir et ne peut donc ainsi être un ascendant de u.
Complexité
Notons n le nombre de nœuds de l'arbre et m la cardinalité de l'ensemble des couples C.
Si l'on suppose que la complexité globale de toutes les exécutions de de l'instruction pour chaque nœud w tel que {u,w}… est égale à kitxmlcodeinlinelatexdvpO(m)finkitxmlcodeinlinelatexdvp (voir exercice), toutes les instructions liées aux appels de fonction union, representant, couleur, ascendant sont de complexité en temps constant. Le nombre d'appels récursifs de la fonction parcours est kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp. La complexité en temps est donc kitxmlcodeinlinelatexdvpO(n + m)finkitxmlcodeinlinelatexdvp. L'algorithme est donc linéaire.
Exercice 23 En choisissant une structure appropriée pour représenter l'ensemble C, faites en sorte que la complexité globale de toutes les exécutions de de l'instruction pour chaque nœud w tel que {u,w}… soit kitxmlcodeinlinelatexdvpO(m)finkitxmlcodeinlinelatexdvp.
9. Remerciements▲
Nous tenons à remercier Claude LELOUP pour la relecture orthographique.



